Addition de fractions : méthode claire et fiches d’exercices à imprimer (PDF) avec corrigés

Addition de fractions à imprimer : si vous cherchez une méthode simple, des exemples concrets et des fiches PDF prêtes à télécharger, vous êtes au bon endroit.

Petite histoire d’enseignante

Un jour, en classe, je demande : « Combien font 1/2 + 1/4 ? »
Un élève, très sûr de lui, me répond : « 2/6 ».

Ce n’était pas la bonne réponse, mais c’était une erreur intéressante. Beaucoup d’élèves font la même chose : ils additionnent directement le haut et le bas. J’ai alors expliqué que pour additionner des fractions, il fallait d’abord les exprimer avec le même dénominateur. L’erreur de cet élève est devenue une occasion parfaite pour toute la classe de comprendre la règle fondamentale.

Ce que vous allez apprendre

Dans cet article, vous découvrirez comment :

1. Reconnaître quand les dénominateurs sont identiques et additionner correctement.
   
2. Mettre deux fractions au même dénominateur lorsque l’un est un multiple de l’autre.
   
3. Utiliser le PPCM pour additionner des fractions aux dénominateurs vraiment différents.
   
4. Travailler avec des cas particuliers comme les entiers et les nombres mixtes.
   
5. Visualiser les calculs avec des schémas et sur une droite numérique.
   
6. Vous entraîner avec des exercices progressifs et vérifier vos réponses dans un corrigé.

Vos fiches gratuites à imprimer (PDF)

Prêt à mettre en pratique ? Téléchargez directement nos fiches d’exercices, classées par niveaux, ainsi qu’un corrigé complet.

 Télécharger la Fiche 1 : Niveau Facile (PDF)
Idéal pour commencer avec les dénominateurs identiques.

 Télécharger la Fiche 2 : Niveau Intermédiaire (PDF)
Pour s’entraîner quand un dénominateur est un multiple de l’autre.

 Télécharger la Fiche 3 : Niveau Avancé (PDF)
Le défi final avec dénominateurs différents et simplification.

Table of Contents

Table of Contents

Qu’est-ce qu’une fraction ?

Définition simple

Une fraction est une manière de représenter une partie d’un tout.

• Le numérateur (en haut) indique combien de parts on prend.
  
• Le dénominateur (en bas) indique en combien de parts égales le tout est divisé.

Exemple :

3/4 signifie que l’on prend 3 parts sur 4.

Exemple concret avec une pizza

Imaginez une pizza découpée en 4 parts égales. Si vous en mangez 3, vous avez mangé 3/4 de la pizza.

Pourquoi apprendre à additionner des fractions ?

L’addition de fractions ne sert pas seulement en cours de mathématiques. Elle s’applique dans la vie de tous les jours :

• En cuisine : additionner des mesures (ex. 1/2 litre + 1/4 litre).
  
• Dans le temps : additionner des durées (ex. 3/4 d’heure + 2/3 d’heure).
  
• Dans le partage : additionner des parts de gâteau ou de chocolat.

Règle de base : toujours un dénominateur commun

Avant d’additionner des fractions, il faut que les dénominateurs soient identiques. C’est la règle essentielle qui évite les erreurs.

La règle essentielle

• On additionne uniquement les numérateurs (les nombres du haut).
  
• On garde le même dénominateur (le nombre du bas).

On ne doit jamais additionner directement le haut et le bas.

1/2 + 1/2 = 2/2 = 1

Ici, les dénominateurs sont déjà identiques (2), donc on additionne seulement les numérateurs.

Exemple d’erreur fréquente

Certains élèves écrivent :

1/2 + 1/4 = 2/6

Cette réponse est fausse, car les dénominateurs (2 et 4) sont différents. Avant d’additionner, il faut transformer les fractions pour qu’elles aient le même dénominateur.

Encadré pédagogique

À retenir :

1. On n’additionne jamais directement le haut et le bas.
   
2. Les fractions doivent toujours avoir un dénominateur commun avant d’être additionnées.
   
3. Une fois les dénominateurs identiques, on additionne seulement les numérateurs.

  Cette règle est la base de toutes les méthodes que nous allons voir ensuite. La première situation, la plus simple, est quand les fractions ont déjà le même dénominateur.

Cas 1 : Addition de fractions avec le même dénominateur

C’est la situation la plus simple : lorsque les fractions ont déjà le même dénominateur.

La méthode pas à pas

1. Vérifiez que les dénominateurs sont identiques.
   
2. Additionnez uniquement les numérateurs.
   
3. Conservez le dénominateur.

Exemple :

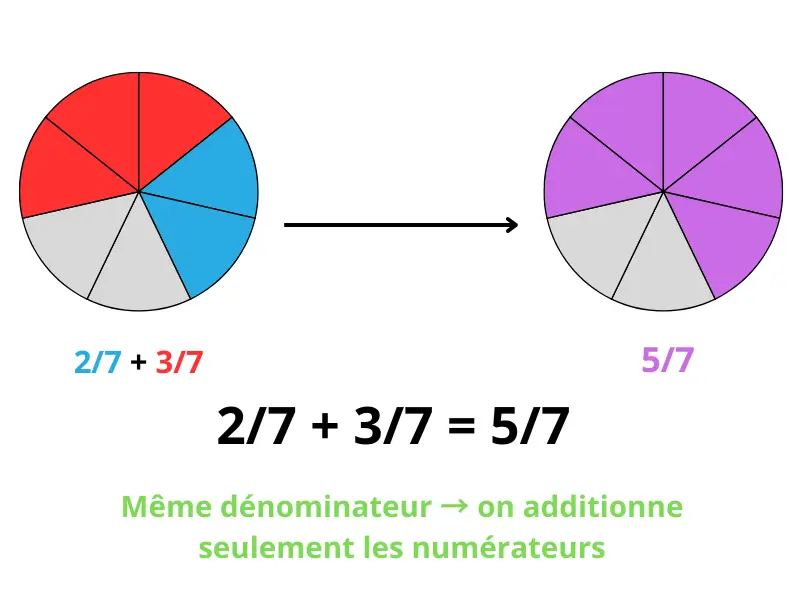
2/7 + 3/7

• Les dénominateurs sont identiques (7).
  
• On additionne les numérateurs : 2 + 3 = 5.
  
• Résultat : 5/7.

Cas 2 : Addition de fractions avec un dénominateur multiple de l’autre

Il arrive souvent qu’un des dénominateurs soit un multiple direct de l’autre. Dans ce cas, il suffit de transformer une seule fraction pour qu’elles aient le même dénominateur.

La méthode pas à pas

1. Repérez le dénominateur le plus grand.
2. Transformez la fraction avec le plus petit dénominateur pour l’exprimer sur le plus grand.
3. Additionnez les numérateurs.
4. Simplifiez si nécessaire.

Exemple :

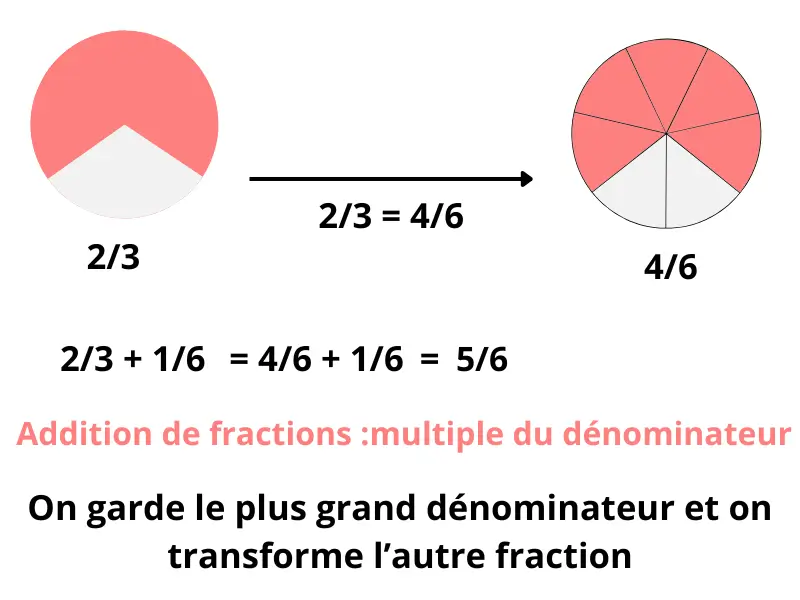
On veut calculer : 2/3 + 1/6

1. Le dénominateur 6 est un multiple de 3.
2. On transforme 2/3 en 4/6.
3. On additionne : 4/6 + 1/6 = 5/6.

Résultat : 5/6

Cas 3 : Addition de fractions avec des dénominateurs différents (PPCM)

C’est le cas le plus général et celui qui demande un peu plus de travail. Lorsque les dénominateurs ne sont pas des multiples l’un de l’autre, il faut trouver un dénominateur commun. Pour cela, on utilise le Plus Petit Commun Multiple (PPCM).

Pourquoi utiliser le PPCM ?

On pourrait multiplier directement les deux dénominateurs pour trouver un dénominateur commun. Mais cela donne parfois des nombres trop grands, donc plus compliqués à simplifier.
  En utilisant le PPCM, on choisit le plus petit multiple commun aux deux dénominateurs, ce qui permet de travailler avec des nombres plus simples et de réduire les calculs.

Exemple :

• Pour 1/3 + 1/4, multiplier 3 × 4 = 12 → le PPCM est 12, c’est parfait.
  
• Pour 6 et 8, multiplier donne 48, mais le PPCM est 24, ce qui évite de manipuler de grands nombres.

La méthode pas à pas

1. Trouver le PPCM des deux dénominateurs.
   
2. Transformer chaque fraction en fraction équivalente avec ce dénominateur.
   
3. Additionner les numérateurs.
   
4. Simplifier si possible.

Exemple :

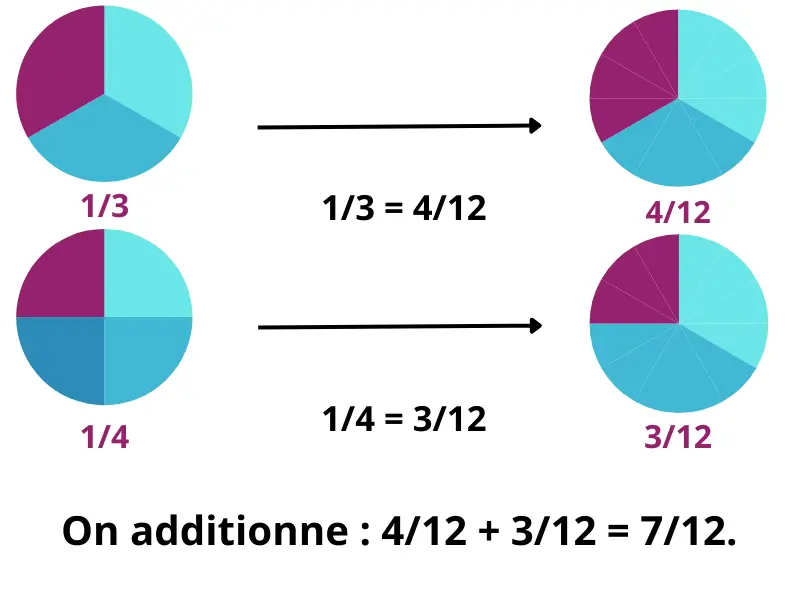
On veut calculer : 1/3 + 1/4

1. Le PPCM de 3 et 4 est 12.
2. On transforme : 1/3 = 4/12 et 1/4 = 3/12.
3. On additionne : 4/12 + 3/12 = 7/12.

Résultat : 7/12

Représentations visuelles pour mieux comprendre

Les fractions deviennent plus faciles à comprendre quand on les visualise. Deux représentations sont particulièrement utiles : la droite numérique et les schémas de parts (pizzas, rectangles).

1. Sur une droite numérique

Exemple :

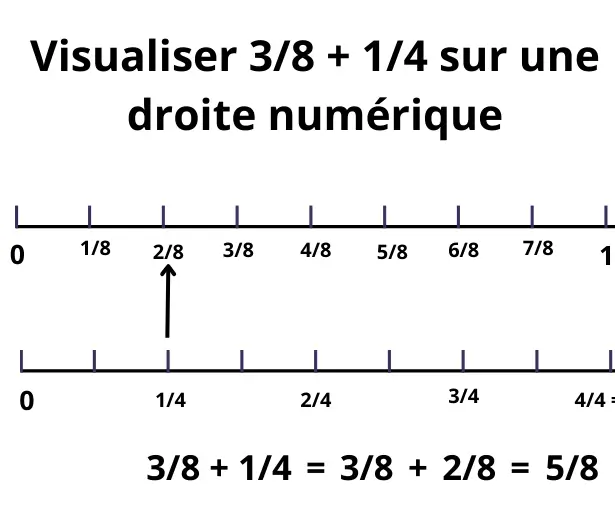
On veut calculer : 3/8 + 1/4

1. On choisit un dénominateur commun : 8.
2. On place 3/8 sur la droite graduée en huitièmes.
3. On transforme 1/4 en 2/8.
4. À partir de 3/8, on avance de 2 graduations → on arrive à 5/8.

Résultat : 5/8

2. Avec des schémas (pizzas ou rectangles)

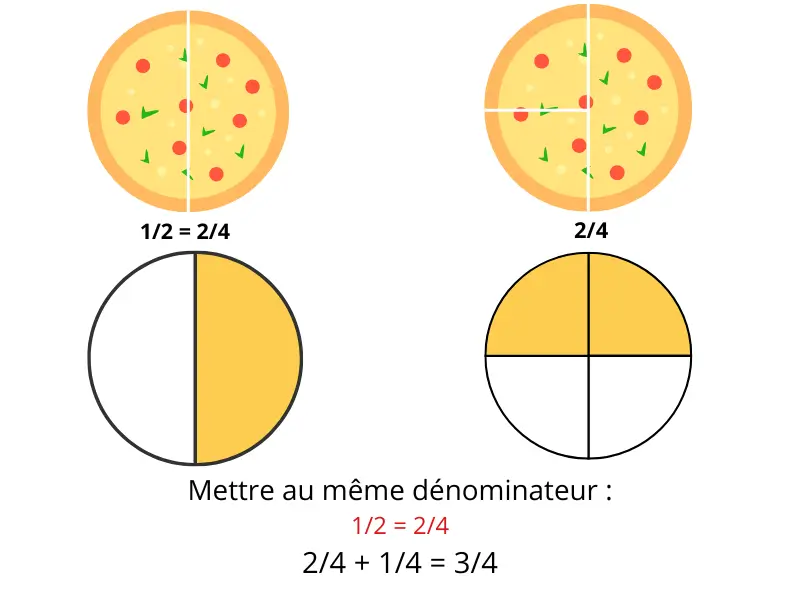
On veut calculer : 1/2 + 1/4

1. Un cercle divisé en 2 parts → on en prend une (1/2).
2. Un cercle divisé en 4 parts → on en prend une (1/4).
3. En transformant 1/2 en 2/4, on obtient : 2/4 + 1/4 = 3/4

Résultat : 3/4

Étape finale : simplifier les fractions

Une fois l’addition terminée, il est indispensable de vérifier si la fraction obtenue peut être simplifiée. On parle de fraction irréductible lorsque le numérateur et le dénominateur n’ont plus de diviseur commun autre que 1.

Pourquoi simplifier ?

• Pour rendre le résultat plus lisible et facile à comprendre.
• Parce que les corrigés et manuels présentent toujours les fractions sous leur forme la plus simple.
• Exemple : 2/4 est correct, mais on attend généralement 1/2.

Exemple 1 :

On veut simplifier la fraction 6/10.

• Numérateur et dénominateur sont divisibles par 2.
• En divisant par 2 : 6/10 = 3/5.

Résultat : 3/5

Exemple 2 (après une addition) :

On a calculé : 1/6 + 2/6 = 3/6

• On simplifie en divisant par 3 :
  3/6 = 1/2

Résultat : 1/2

Vos fiches d’exercices gratuites à imprimer (PDF)

Apprendre les fractions passe avant tout par la pratique. Pour vous aider, j’ai préparé des fiches d’exercices progressives à télécharger et à imprimer, ainsi qu’un corrigé complet pour s’auto-évaluer.

Téléchargez vos fiches.

Télécharger la Fiche 1 : Niveau Facile (PDF)
Idéal pour commencer avec les fractions qui ont le même dénominateur.

Niveau FacileTélécharger

Télécharger la Fiche 2 : Niveau Intermédiaire (PDF)
Pour s’exercer quand un dénominateur est un multiple de l’autre .

Niveau IntermédiaireTélécharger

Télécharger la Fiche 3 : Niveau Avancé (PDF)
Le défi final : addition de fractions avec dénominateurs totalement différents (PPCM) et simplification.

Niveau AvancéTélécharger

Problèmes concrets d’addition de fractions

L’addition de fractions n’est pas seulement un exercice scolaire. On la retrouve dans de nombreuses situations de la vie quotidienne. Voici quelques exemples pratiques.

Exemple avec de la nourriture

• Situation :
  • “Un enfant mange 1/4 de pizza, un autre mange 2/4. Combien ont-ils mangé ensemble ?”
  • Résultat : 3/4 de pizza.

Exemple avec du temps

• Situation :
  • “Tu passes 1/2 heure à lire et 1/4 d’heure à écrire. Combien de temps en tout ?”
  • Résultat : 3/4 d’heure.

Exemple avec des liquides

• Situation :
  • “Un verre contient 1/3 d’eau, un autre 2/3. Combien d’eau en tout ?”
  • Résultat : 1 verre plein (3/3 = 1).

Conclusion

L’addition de fractions repose toujours sur une seule idée essentielle : avoir un dénominateur commun.

• Quand les dénominateurs sont identiques, on additionne directement les numérateurs.
  
• Quand l’un est un multiple de l’autre, on transforme une seule fraction.
  
• Quand ils sont totalement différents, on utilise le PPCM.

Enfin, on pense toujours à simplifier le résultat pour obtenir une fraction irréductible.

Grâce aux exemples, aux schémas visuels et aux exercices progressifs proposés dans cet article, vous disposez désormais de toutes les clés pour comprendre et réussir l’addition de fractions.

Pour progresser encore plus vite, n’hésitez pas à utiliser les fiches d’exercices PDF à imprimer mises à votre disposition, avec corrigés séparés. Elles permettent de s’entraîner en autonomie, comme en classe.

Apprendre les fractions ne doit pas être source de stress : avec une méthode claire et beaucoup de pratique, cette notion devient simple et même utile au quotidien.

Pensez à sauvegarder et partager nos fiches d’exercices sur Pinterest pour y revenir facilement plus tard, et pour aider d’autres élèves à progresser !

FAQ sur l’Addition de Fractions