L’aire du losange est une notion importante en géométrie au cycle CM2–6e. Elle permet de calculer une surface en utilisant uniquement les diagonales, ce qui est très utile lorsque la hauteur n’est pas donnée dans l’énoncé. La méthode est simple à comprendre grâce à une observation géométrique facile à réaliser et à une démonstration visuelle qui montre clairement pourquoi la formule fonctionne. Cette leçon propose une explication complète, suivie d’exemples détaillés, des erreurs fréquentes et d’exercices avec leurs corrections.
Table of Contents
Qu’est-ce qu’un losange ?
Un losange est un quadrilatère particulier dont les quatre côtés sont de même longueur. Contrairement au carré, ses angles ne sont pas forcément droits. Le losange peut être allongé, incliné ou aplati : ce qui ne change jamais, c’est l’égalité de ses côtés.
Propriétés importantes du losange
Les quatre côtés sont égaux.
Les angles opposés ont la même mesure.
Les diagonales se coupent en leur milieu et sont perpendiculaires.
Les diagonales jouent un rôle essentiel pour calculer son aire.
Un losange ressemble à un carré que l’on aurait légèrement “incliné”.
Les diagonales du losange
Un losange possède deux diagonales, chacune reliant deux sommets opposés. Elles se croisent en leur milieu et forment un angle droit.
On les note généralement :
D : la grande diagonale
d : la petite diagonale
Dans le calcul de l’aire, ce sont les diagonales D et d qui fournissent toutes les informations nécessaires.
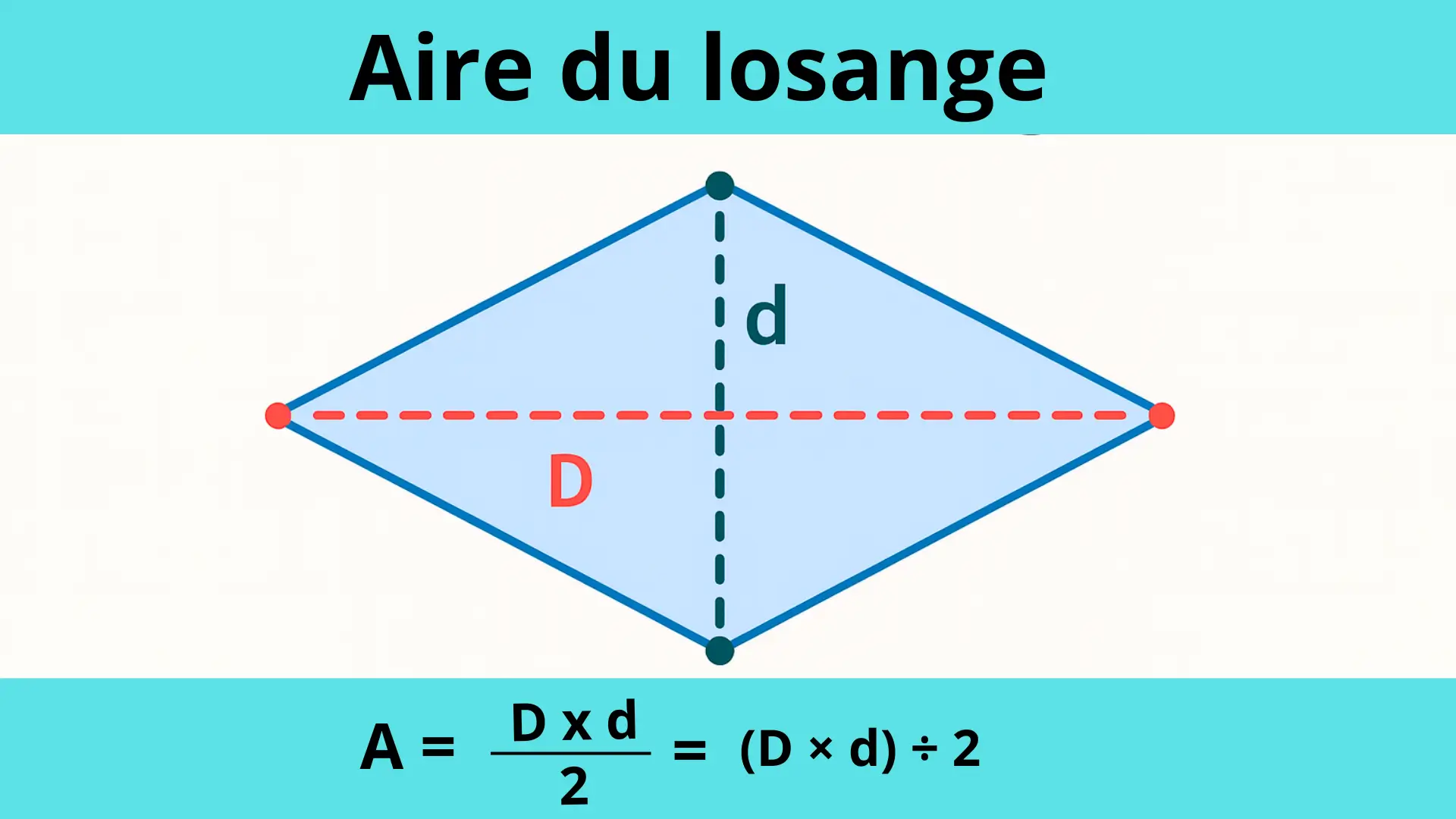
Formule de l’aire du losange
L’aire d’un losange se calcule grâce à ses deux diagonales, et non à partir de ses côtés. La formule est la suivante : A = (D × d) ÷ 2 ou A = (D × d) / 2.
D est la grande diagonale du losange.
d est la petite diagonale du losange.
A est l’aire.
L’aire du losange correspond à la moitié du produit des deux diagonales.
Pourquoi la formule fonctionne
Pour comprendre cette formule, on peut utiliser une construction géométrique simple. On dessine un rectangle, puis on trace un losange en reliant les milieux des côtés du rectangle. Cette construction crée quatre triangles identiques dans les coins du rectangle, ainsi qu’un losange central.
Les quatre triangles ont la même forme et la même aire. Si on les découpe et qu’on les assemble, ils forment un deuxième losange identique à celui du centre. On obtient donc un rectangle composé de deux losanges identiques.
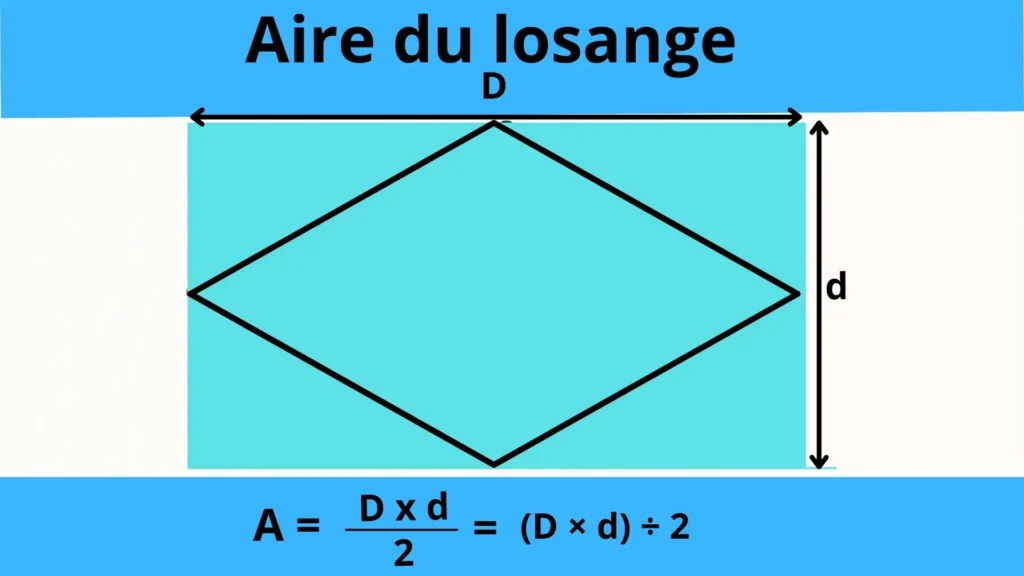
Dans cette configuration :
La longueur du rectangle correspond à la grande diagonale du losange (D).
La largeur du rectangle correspond à la petite diagonale du losange (d).
Ainsi :
Aire du rectangle = D × d
Aire du losange = Aire du rectangle ÷ 2
Aire du losange = (D × d) ÷ 2
Cette démonstration simple, basée sur le découpage et la recomposition des triangles, explique clairement pourquoi la formule de l’aire du losange est la moitié du produit de ses deux diagonales.
Étapes pour calculer l’aire du losange
Étape 1 : Identifier les deux diagonales D et d.
Étape 2 : Calculer le produit D × d.
Étape 3 : Diviser ce résultat par 2.
Étape 4 : Écrire l’aire avec l’unité correcte (cm², mm², m², etc.).
Exemples d’application
Exemple 1
D = 6 cm
d = 4 cm
A = (6 × 4) ÷ 2 = 12 cm²
Exemple 2
D = 15 cm
d = 10 cm
A = (15 × 10) ÷ 2 = 75 cm²
Exemple 3
D = 8 dm
d = 120 cm
120 cm = 12 dm
A = (8 × 12) ÷ 2 = 48 dm²
Les erreurs les plus fréquentes des élèves
Confondre les diagonales avec les côtés.
Oublier de diviser par 2.
Utiliser des unités différentes.
Intervertir les valeurs en confondant D et d.
Écrire une unité sans carré (cm au lieu de cm²).
Exercices pour s’entraîner
Exercice 1
D = 8 cm et d = 5 cm. Calculer l’aire.
Exercice 2
D = 12 cm et d = 9 cm. Trouver l’aire.
Exercice 3
D = 7 cm et d = 14 cm. Calculer l’aire.
Exercice 4
D = 25 mm et d = 4 cm. Convertir puis calculer.
Exercice 5
Un losange doit avoir une aire de 40 cm². On connaît D = 10 cm. Trouver d.
Exercice 6
Un terrain en forme de losange possède D = 20 m et d = 32 m. Calculer l’aire.
Exercices corrigés
Exercice 1
D = 8 cm
d = 5 cm
A = (8 × 5) ÷ 2 = 20 cm²
Exercice 2
D = 12 cm
d = 9 cm
A = (12 × 9) ÷ 2 = 54 cm²
Exercice 3
D = 7 cm
d = 14 cm
A = (7 × 14) ÷ 2 = 49 cm²
Exercice 4
D = 25 mm
d = 40 mm
A = (25 × 40) ÷ 2 = 500 mm²
Exercice 5
A = 40 cm²
D = 10 cm
40 = (10 × d) ÷ 2
80 = 10 × d
d = 8 cm
Exercice 6
D = 20 m
d = 32 m
A = (20 × 32) ÷ 2 = 320 m²
Conclusion
Le calcul de l’aire du losange devient simple dès que l’on comprend le rôle essentiel des diagonales. La formule repose sur une observation géométrique intuitive : deux losanges identiques forment un rectangle dont les dimensions correspondent aux diagonales. Les exemples et les exercices proposés permettent de consolider cette méthode et de développer de bons automatismes.
Retrouve CoursCool sur Pinterest pour accéder chaque semaine à de nouvelles fiches d’exercices, affiches de géométrie et astuces de classe qui rendent le calcul d’aire du losange plus simple et motivant pour les élèves de CM2.
Conseil du professeur
Toujours commencer par identifier les diagonales et vérifier qu’elles sont exprimées dans la même unité. Pour renforcer la compréhension, il est utile de reproduire la démonstration avec un découpage réel : les élèves voient ainsi que les quatre triangles peuvent être recomposés pour former un deuxième losange. Cette manipulation simple aide à fixer durablement la formule.
FAQ sur l’aire du losange
Comment reconnaître les diagonales
Les diagonales relient des sommets opposés et se coupent à angle droit.
Quelle unité utiliser
Toujours une unité carrée : cm², mm², dm² ou m².
Peut-on utiliser les côtés
Non, les côtés ne suffisent pas pour calculer l’aire.
Pourquoi diviser par 2
Parce que deux losanges identiques composent le rectangle formé par les diagonales.
Les diagonales doivent-elles être dans la même unité
Oui, sinon l’aire sera fausse.
Comment calcule-t-on l’aire d’un carré ?
L’aire d’un carré se calcule en multipliant la longueur d’un côté par lui-même.
Si le côté mesure c, alors :
Aire du carré = c × c = c²
Comment calcule-t-on l’aire d’un rectangle ?
L’aire d’un rectangle se calcule en multipliant sa longueur par sa largeur.
Si la longueur est L et la largeur est l, alors :
Aire du rectangle = L × l
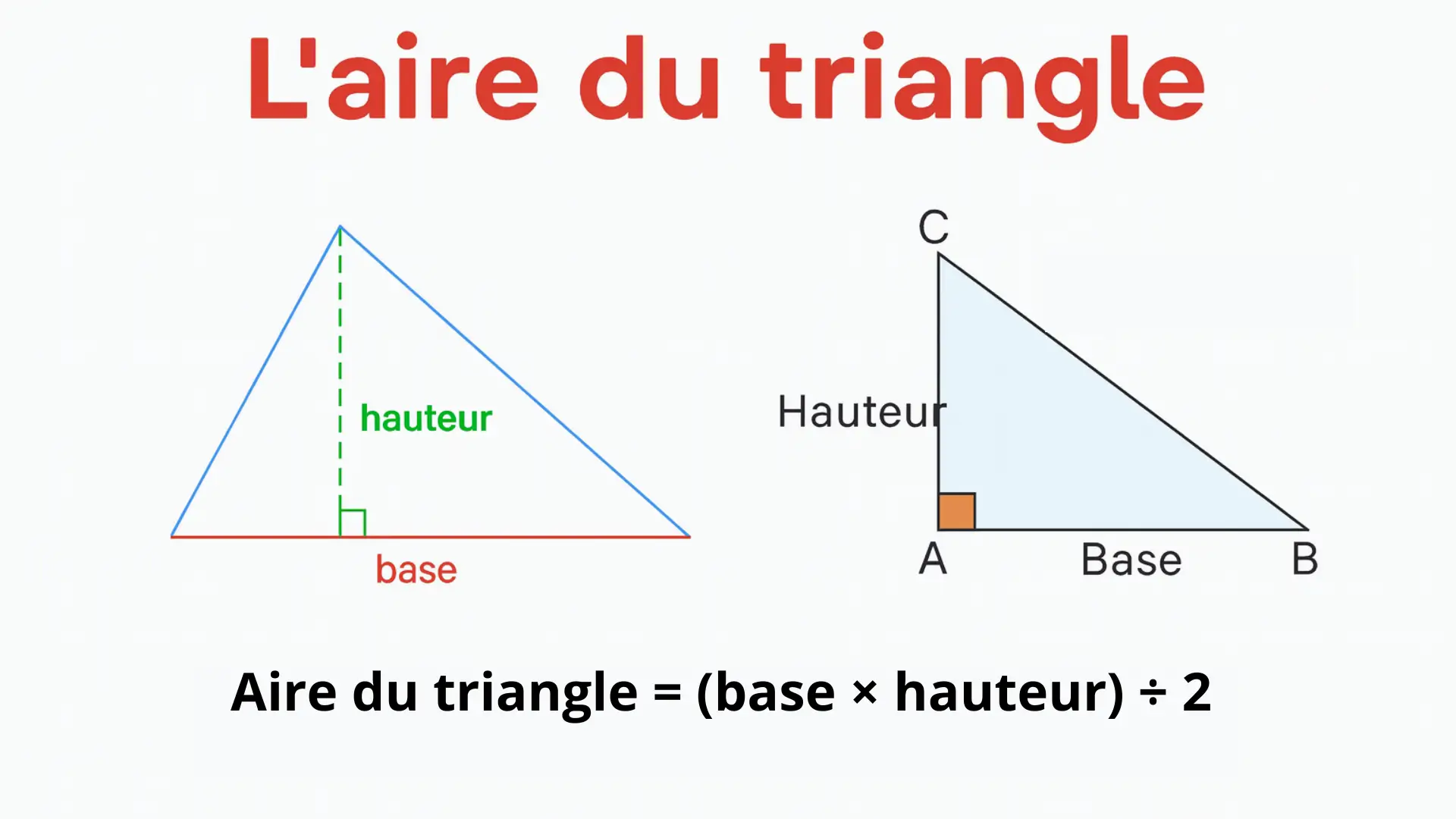
Comment calcule-t-on l’aire d’un triangle ?
L’aire d’un triangle se calcule en multipliant sa base par sa hauteur, puis en divisant le résultat par 2.
Si la base est b et la hauteur est h, alors :
Aire du triangle = (b × h) ÷ 2