Calcul d’aire du triangle voici une notion importante que tous les élèves de CM2 doivent maîtriser avant l’entrée au collège. L’aire d’un triangle peut sembler compliquée au premier regard, surtout lorsque la hauteur n’est pas directement visible ou lorsque les triangles semblent tous différents. Pourtant, avec une méthode claire, des exemples bien expliqués et quelques astuces, cette compétence devient simple, logique… et même amusante !
Comprendre comment calculer l’aire permet aux élèves de développer leur sens de la géométrie, d’apprendre à observer une figure, à identifier la base, à repérer la hauteur et à effectuer un calcul structuré. Ce sont des compétences essentielles pour réussir en mathématiques, mais aussi dans la vie quotidienne : mesurer une surface, construire un objet, comprendre un plan, résoudre un problème concret…
Dans cet article pensé spécialement pour les élèves de CM2, nous allons avancer pas à pas :
- d’abord en découvrant la formule,
- puis en apprenant à reconnaître la base et la hauteur,
- avant de s’entraîner avec des exemples guidés,
- et enfin en appliquant la méthode à des situations réelles.
Tu verras : avec de l’entraînement, le calcul d’aire du triangle devient une compétence facile, presque automatique. Et si une difficulté apparaît, les sections “erreurs fréquentes”, “conseils pour parents et professeurs” et la FAQ t’aideront à tout comprendre sans stress.
Prêt(e) ? C’est parti pour devenir un(e) champion(ne) du calcul d’aire du triangle !
Table of Contents
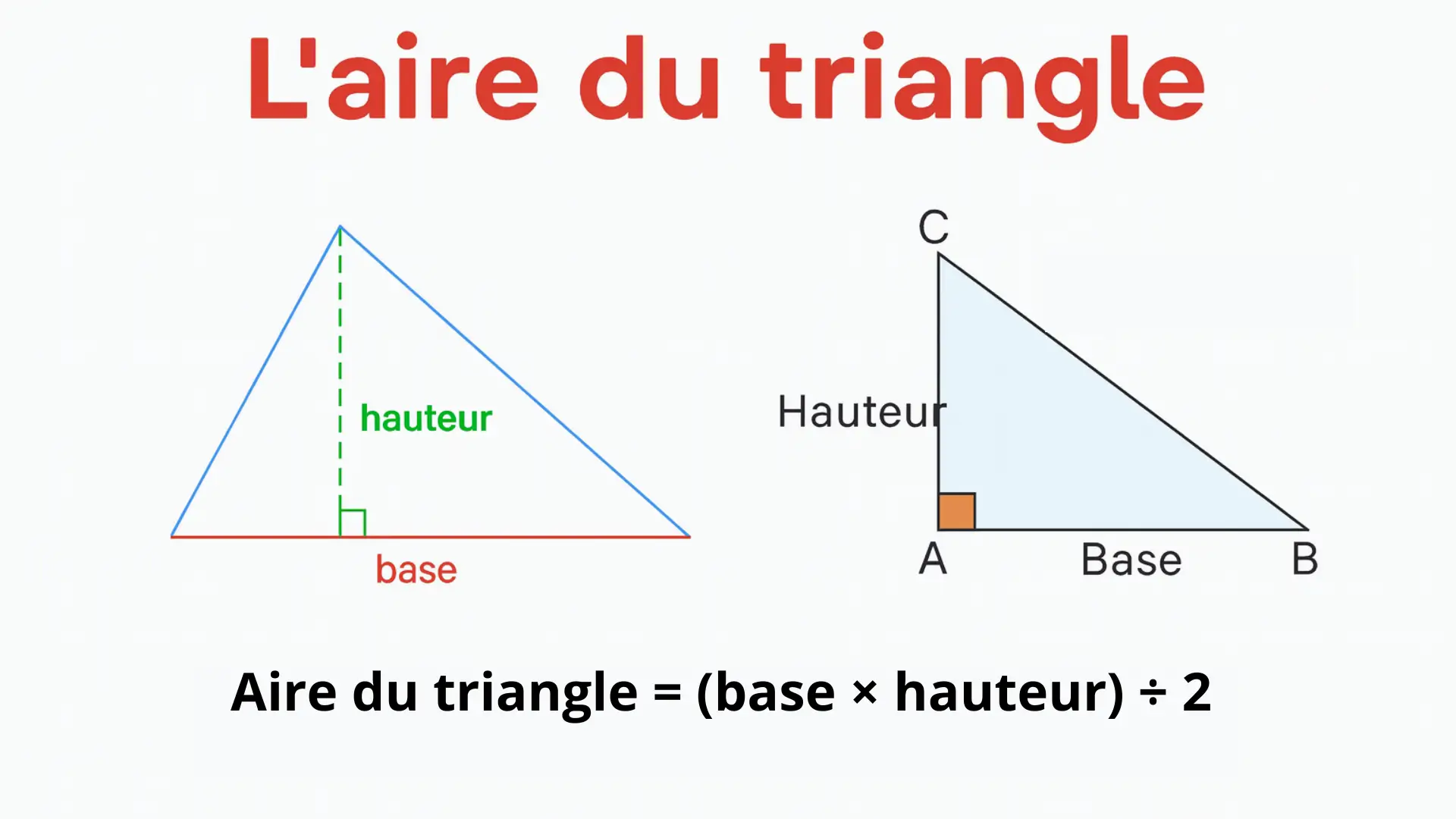
La formule pour calculer l’aire du triangle
Pour trouver l’aire d’un triangle, on utilise une formule simple et toujours la même, quel que soit le type de triangle. L’aire représente la surface du triangle, c’est-à-dire tout l’espace qu’il occupe.
Voici la formule à connaître :
Aire du triangle = (base × hauteur) ÷ 2
La base est le côté du triangle sur lequel on s’appuie pour faire le calcul. On peut choisir n’importe quel côté comme base. La hauteur correspond à la distance perpendiculaire entre cette base et le sommet opposé. La hauteur forme toujours un angle droit avec la base.
Pour bien comprendre, il est important de retenir que la hauteur n’est pas forcément un côté du triangle. Dans un triangle rectangle, elle peut correspondre à un des côtés qui forment l’angle droit. Mais dans un triangle qui n’est pas rectangle, elle peut être dessinée à l’intérieur ou même à l’extérieur du triangle.
Cette formule fonctionne parce qu’un triangle représente exactement la moitié d’un rectangle ou d’un parallélogramme ayant la même base et la même hauteur. C’est pour cette raison que l’on divise par deux à la fin du calcul.
Si tu identifies correctement la base et la hauteur, alors l’aire du triangle sera toujours facile à trouver.
Pourquoi l’aire du triangle est la moitié d’un rectangle
Pour comprendre la formule de l’aire du triangle, on peut partir d’un rectangle, une figure que les élèves connaissent bien. L’aire d’un rectangle se calcule en multipliant :
Aire du rectangle = longueur × largeur
Si l’on découpe ce rectangle en traçant une diagonale, on obtient deux triangles parfaitement identiques. Chaque triangle représente exactement la moitié de la surface du rectangle.
Dans cette situation, la longueur du rectangle joue le rôle de base du triangle et la largeur du rectangle joue le rôle de hauteur du triangle. Autrement dit, les dimensions du rectangle deviennent les deux mesures nécessaires pour calculer l’aire du triangle.
Ainsi, comme chaque triangle correspond à la moitié du rectangle, son aire se calcule avec la formule :
Aire du triangle = (base × hauteur) ÷ 2
Cette manière d’observer le rectangle permet aux élèves de comprendre pourquoi on divise par deux. Ils visualisent que le triangle n’est qu’une moitié de rectangle.

Comment reconnaître la base et la hauteur ?
Pour calculer l’aire d’un triangle, il est indispensable d’identifier correctement la base et la hauteur. Ce sont les deux mesures qui permettent d’appliquer la formule. Pourtant, beaucoup d’élèves confondent parfois un côté avec la hauteur, surtout lorsque celle-ci n’est pas directement visible dans la figure. Voici comment s’y retrouver facilement.
Dans un triangle rectangle
Un triangle rectangle possède un angle droit. Les deux côtés qui forment cet angle droit sont perpendiculaires l’un à l’autre. L’un de ces côtés peut être choisi comme base et l’autre devient alors la hauteur. Dans ce type de triangle, reconnaître la hauteur est simple, car elle correspond à un des côtés du triangle.
Exemple : si un triangle rectangle a un angle droit entre deux côtés mesurant 6 cm et 4 cm, ces deux côtés jouent le rôle de base et de hauteur.
Dans un triangle qui n’est pas rectangle
Dans un triangle quelconque (non rectangle), la hauteur n’est pas un côté du triangle. Elle doit être tracée. Pour la trouver, on choisit d’abord un côté comme base. À partir du sommet opposé, on trace une droite perpendiculaire à cette base. La distance entre ce sommet et la base est la hauteur.
Parfois, la hauteur se trouve à l’intérieur du triangle, mais elle peut aussi être extérieure. Cela arrive lorsque la base choisie est plus longue que le triangle lui-même. Dans ce cas, la hauteur sera tracée en dehors de la figure.
Astuces pour ne pas se tromper
Pour bien reconnaître la hauteur, il faut vérifier qu’elle forme un angle droit avec la base. Si ce n’est pas le cas, ce n’est pas la hauteur. Une bonne façon de vérifier est d’imaginer ou de tracer un petit carré à l’endroit où la hauteur touche la base : s’il est possible d’y dessiner un angle droit, alors la mesure est correcte.
Identifying la base et la hauteur correctement garantit que le calcul de l’aire sera juste. Une fois ces deux mesures repérées, il ne reste plus qu’à appliquer la formule.
Exemples de calcul de l’aire du triangle (niveau CM2)
Dans cette partie, nous allons appliquer la formule de l’aire en utilisant deux types de triangles : un triangle rectangle et un triangle quelconque. Ces exemples montrent aux élèves comment utiliser correctement la base, la hauteur et la division par deux.
Exemple 1 : Triangle rectangle
On considère un triangle rectangle dont les deux côtés perpendiculaires mesurent 8 cm et 5 cm.
Base : 8 cm
Hauteur : 5 cm
Aire du triangle = (base × hauteur) ÷ 2
Aire = (8 × 5) ÷ 2
Aire = 40 ÷ 2
Aire = 20 cm²
L’aire de ce triangle rectangle est donc de 20 cm².
Exemple 2 : Triangle quelconque
On considère un triangle dont la base mesure 12 cm. La hauteur correspondant à cette base est de 7 cm. Cette hauteur est tracée perpendiculairement depuis le sommet opposé.
Base : 12 cm
Hauteur : 7 cm
Aire du triangle = (base × hauteur) ÷ 2
Aire = (12 × 7) ÷ 2
Aire = 84 ÷ 2
Aire = 42 cm²
L’aire de ce triangle quelconque est donc de 42 cm².
Exemple 3 : Triangle avec hauteur extérieure
On prend un triangle dont la base mesure 9 cm. La hauteur mesurée à partir du sommet opposé est extérieure au triangle et vaut 6 cm.
Base : 9 cm
Hauteur : 6 cm
Aire du triangle = (9 × 6) ÷ 2
Aire = 54 ÷ 2
Aire = 27 cm²
Même si la hauteur est extérieure, le calcul reste exactement le même.
Ces exemples montrent que la méthode ne change pas selon la position de la hauteur. Une fois la base et la hauteur bien identifiées, l’aire se calcule toujours de la même manière.
Comment vérifier si son résultat est correct ?
Lorsque l’on calcule l’aire d’un triangle, il est important de vérifier si le résultat obtenu est logique. Cela permet d’éviter les erreurs les plus courantes et de s’assurer que la méthode a été correctement appliquée. Voici plusieurs façons simples de vérifier un calcul.
Comparer avec un rectangle
Un triangle peut être considéré comme la moitié d’un rectangle. Pour savoir si le résultat est raisonnable, on peut imaginer un rectangle complet ayant la même base et la même hauteur que le triangle.
Si la base est de 10 cm et la hauteur de 6 cm, le rectangle correspondant aurait une aire de 10 × 6 = 60 cm². Comme le triangle représente la moitié, son aire doit être proche de 30 cm².
Si le résultat obtenu est très éloigné de cette valeur, il est utile de refaire le calcul.
Vérifier la hauteur
La hauteur doit toujours être perpendiculaire à la base. Avant de vérifier le calcul, il faut s’assurer que la mesure utilisée est bien la hauteur. Si la hauteur choisie n’est pas correcte, alors le calcul sera faux.
Pour vérifier, on peut se demander : « Est-ce que la hauteur forme un angle droit avec la base ? »
Regarder les unités
Il est essentiel d’utiliser les mêmes unités pour la base et la hauteur. Si l’unité de la base est en centimètres et celle de la hauteur en mètres, le calcul sera incorrect. Il faut donc convertir les unités avant de multiplier.
Recalculer rapidement
Une dernière vérification consiste à refaire rapidement le calcul mentalement. Par exemple, si la base mesure 8 cm et la hauteur 4 cm, on peut se dire que 8 × 4 = 32, puis diviser par deux pour obtenir 16. Si le premier calcul donnait 32 ou 4, il est évident qu’une erreur s’est glissée.
Ces vérifications simples aident les élèves à gagner en autonomie et à s’assurer que leur résultat est juste avant de passer à l’exercice suivant.
Exercices pour s’entraîner (CM2)
Ces exercices permettent aux élèves d’appliquer la formule de l’aire du triangle dans différentes situations. Les données sont simples et adaptées au niveau CM2. Les élèves doivent identifier la base, repérer la hauteur et utiliser correctement la division par deux.
Exercice 1 : Triangle rectangle
Un triangle rectangle possède deux côtés perpendiculaires mesurant 9 cm et 6 cm.
Calcule l’aire de ce triangle.
Exercice 2 : Triangle quelconque
Un triangle a pour base 14 cm. La hauteur correspondant à cette base mesure 5 cm.
Calcule l’aire de ce triangle.
Exercice 3 : Hauteur extérieure
Un triangle a pour base 11 cm. La hauteur mesurée à partir du sommet opposé est extérieure et vaut 8 cm.
Calcule l’aire de ce triangle.
Exercice 4 : Situation concrète
Un panneau triangulaire a une base de 20 cm et une hauteur de 12 cm.
Calcule l’aire du panneau.
Exercice 5 : Unités différentes
Un triangle a une base de 0,5 m et une hauteur de 60 cm.
Avant de calculer, convertis les unités pour qu’elles soient identiques.
Calcule ensuite l’aire du triangle.
Les erreurs fréquentes : Calcul d’aire du triangle
Lorsqu’ils apprennent à calculer l’aire d’un triangle, beaucoup d’élèves de CM2 font les mêmes erreurs. Les connaître à l’avance permet de mieux les éviter et de comprendre ce qu’il faut vérifier avant d’écrire le résultat.
Confondre un côté avec la hauteur
Dans un triangle quelconque, la hauteur n’est pas un côté du triangle. Certains élèves choisissent un côté au hasard en pensant que c’est la hauteur, ce qui rend le calcul incorrect. La hauteur doit toujours être perpendiculaire à la base.
Oublier de diviser par deux
Comme le triangle représente la moitié d’un rectangle, il est indispensable de diviser le résultat final par deux. Beaucoup d’élèves multiplient seulement la base par la hauteur et s’arrêtent là.
Utiliser des unités différentes
Il arrive qu’un exercice donne la base en centimètres et la hauteur en mètres. Si on multiplie les deux sans conversion, le résultat n’a pas de sens. Il faut toujours convertir pour obtenir les mêmes unités avant de calculer.
Se tromper de base
Dans certains triangles, plusieurs côtés peuvent être pris comme base. Le choix n’a pas d’importance, mais il faut que la hauteur utilisée corresponde bien à la base choisie. Si la base et la hauteur ne sont pas associées, le calcul est faux.
Mal lire la figure
Certains élèves lisent trop vite la figure et ne voient pas que la hauteur est tracée à l’extérieur du triangle ou qu’elle ne part pas du bon sommet. Une observation attentive est essentielle avant de commencer le calcul.
Connaître ces erreurs permet à l’élève d’être plus vigilant et de mieux réussir ses exercices de géométrie.
Conseils pour les parents et les professeurs
L’apprentissage du calcul de l’aire du triangle peut devenir beaucoup plus simple si l’élève est accompagné de manière progressive et concrète. Voici quelques conseils pratiques pour guider les enfants dans cette notion.
Encourager l’observation avant le calcul
Avant d’écrire la formule, il est essentiel que l’élève prenne le temps de bien regarder la figure. Demander à l’enfant : « Où est la base ? Où est la hauteur ? » permet de développer son sens de l’analyse en géométrie.
Utiliser des objets du quotidien
Un simple cahier, un carton découpé ou une feuille pliée en deux peuvent aider l’élève à comprendre qu’un triangle peut représenter la moitié d’un rectangle. Cette manipulation rend la formule beaucoup plus intuitive.
Varier les types de triangles
Il est important de montrer plusieurs cas : triangle rectangle, triangle avec hauteur intérieure, triangle avec hauteur extérieure. En voyant ces différentes situations, l’élève devient plus autonome et ne se limite pas à un seul type de figure.
Faire verbaliser la méthode
Demander à l’élève d’expliquer sa démarche aide à vérifier s’il a bien compris la notion. Par exemple : « J’ai choisi ce côté comme base, puis j’ai trouvé la hauteur qui est perpendiculaire. Ensuite, je multiplie et je divise par deux. »
Mettre en avant la cohérence des unités
Les élèves oublient souvent de vérifier que la base et la hauteur sont exprimées dans la même unité. Rappeler cette étape permet d’éviter beaucoup d’erreurs.
Proposer des relectures rapides
Après avoir obtenu un résultat, encourager l’élève à vérifier si la réponse semble logique. Comparer avec l’aire d’un rectangle de mêmes dimensions est une méthode simple et efficace.
Ces conseils aident les parents et les professeurs à accompagner les élèves de manière structurée, en renforçant leur compréhension de la géométrie et leur confiance dans la résolution des exercices.
Conclusion et Le mot de la prof
Le calcul de l’aire du triangle est une notion importante du programme de CM2. Elle prépare les élèves aux futures notions de géométrie qu’ils découvriront au collège. Même si cette compétence peut sembler difficile au début, elle devient rapidement simple lorsque la méthode est bien comprise.
Retenir que l’aire d’un triangle correspond à la moitié d’un rectangle permet de donner du sens à la formule. Une fois que l’élève sait repérer la base, trouver la hauteur et vérifier que les unités sont correctes, le calcul devient automatique.
Chaque élève peut réussir cette notion avec un peu d’entraînement et de patience. En géométrie, l’essentiel est d’observer attentivement, de raisonner calmement et de vérifier son résultat. Tous les élèves peuvent progresser et gagner en confiance.
Si tu es élève, n’hésite pas à relire les exemples, à refaire les exercices et à comparer tes résultats avec ceux d’un rectangle pour vérifier la cohérence. Si tu es parent ou professeur, accompagner l’enfant dans ces étapes l’aidera à renforcer sa compréhension.
Comprendre cette notion aujourd’hui, c’est se donner les moyens de réussir en mathématiques demain.
Retrouve CoursCool sur Pinterest pour accéder chaque semaine à de nouvelles fiches d’exercices, affiches de géométrie et astuces de classe qui rendent le calcul d’aire du triangle plus simple et motivant pour les élèves de CM2.
FAQ : Questions fréquentes
Comment trouver la hauteur d’un triangle si elle n’est pas dessinée ?
Il faut d’abord choisir un côté du triangle comme base. Puis, à partir du sommet opposé, on trace une droite perpendiculaire à cette base. La distance entre le sommet et la base est la hauteur. Elle peut être à l’intérieur ou à l’extérieur du triangle.
Est-ce que je peux choisir n’importe quel côté comme base ?
Oui. On peut choisir n’importe quel côté comme base. Mais il faut toujours utiliser la hauteur qui correspond à cette base. Une base et une hauteur ne vont que par paire.
Pourquoi faut-il diviser par deux ?
Parce qu’un triangle représente la moitié d’un rectangle ou d’un parallélogramme ayant la même base et la même hauteur. C’est pour cela que, après avoir multiplié la base par la hauteur, on divise le résultat par deux.
Que faire si la base est en centimètres et la hauteur en mètres ?
Il faut convertir les deux mesures dans la même unité avant de calculer. Par exemple, transformer 0,5 m en 50 cm ou 60 cm en 0,6 m. Ensuite seulement, on applique la formule.
Comment vérifier que mon résultat est correct ?
On peut comparer avec l’aire du rectangle ayant la même base et la même hauteur. On peut aussi refaire le calcul rapidement ou vérifier que la hauteur utilisée est bien perpendiculaire à la base.
Peut-on trouver l’aire d’un triangle si on ne connaît pas la hauteur ?
Non. Pour appliquer la formule de CM2, il faut obligatoirement connaître la base et la hauteur. D’autres méthodes existent au collège, mais elles ne sont pas étudiées en CM2.