L’Aire, c’est quoi au juste ?
Imagine que tu poses ton cahier sur la table et que tu te demandes : “Quelle place occupe-t-il exactement ?”. Cette place, cet espace à l’intérieur du rectangle, c’est ce qu’on appelle l’aire.
Apprendre à mesurer l’ aire est très utile dans la vie quotidienne : pour savoir si un tapis va couvrir le sol de ta chambre, pour comparer deux écrans de tablette ou encore pour calculer la taille d’un petit jardin.
Dans cet article, nous allons découvrir comment calculer l’aire d’un rectangle de façon simple et amusante. Nous allons commencer par compter des petits carreaux comme un jeu, puis passer à une méthode plus rapide grâce à une formule magique : Longueur × Largeur.
À la fin, tu sauras non seulement calculer l’aire facilement, mais aussi comprendre à quoi cela sert dans la vraie vie.
La Réponse en Bref
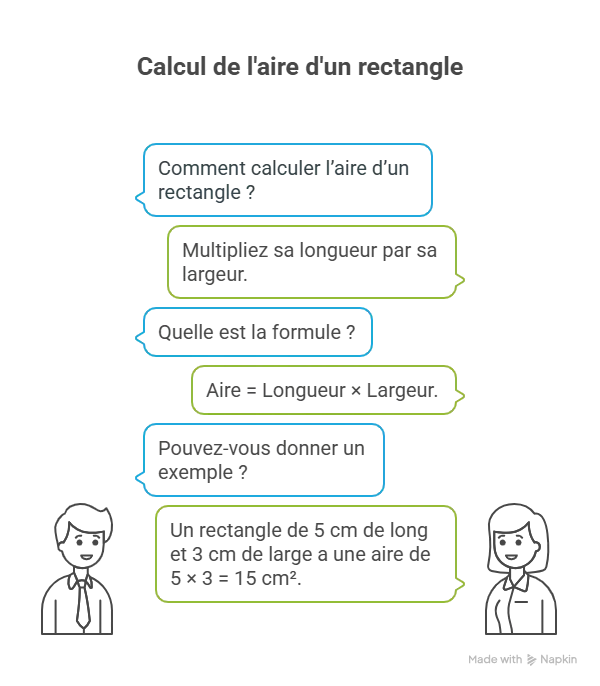
Table of Contents
Table of Contents
Comprendre l’Aire en Comptant des Carreaux
Avant d’apprendre la formule, il est important de comprendre l’aire avec les yeux. Prenons un rectangle dessiné sur un cahier à petits carreaux. Chaque carreau représente une unité de surface : 1 cm² (un centimètre carré).
Pour trouver l’aire du rectangle, il suffit de compter tous les carreaux à l’intérieur.
Exemple concret : un rectangle mesure 4 carreaux de long et 3 carreaux de large. Si on compte tous les petits carrés, on obtient :
- Ligne 1 : 4 carreaux
- Ligne 2 : 4 carreaux
- Ligne 3 : 4 carreaux
Au total, cela fait 12 carreaux. L’aire de ce rectangle est donc 12 cm².
C’est comme si tu remplissais ton rectangle avec de petits autocollants carrés, sans laisser de vide.
De la Grille à la Formule : L’Astuce de la Multiplication
Compter les carreaux un par un, c’est amusant… mais quand le rectangle est très grand, cela devient vite long. Heureusement, il existe une astuce pour aller plus vite : utiliser la multiplication.
Dans l’exemple précédent (rectangle de 4 carreaux de long et 3 carreaux de large), la longueur est de 4 carreaux et la largeur est de 3 carreaux. Le rectangle est formé de 3 rangées de 4 carreaux. Au lieu de les compter un par un, on fait :
Aire = Longueur × Largeur
Aire = 4 × 3 = 12 cm²
C’est exactement le même résultat que lorsqu’on comptait, mais en beaucoup moins de temps.
La formule générale est donc : Aire d’un rectangle = Longueur × Largeur.
La longueur correspond au côté le plus grand. La largeur correspond au côté plus petit. Le résultat s’exprime toujours en unités carrées (cm², m², etc.).
Exemple rapide : un rectangle mesure 8 cm de long et 5 cm de large. Son aire est : 8 × 5 = 40 cm².
Calcul de Surface : 3 Exemples Concrets Pas à Pas
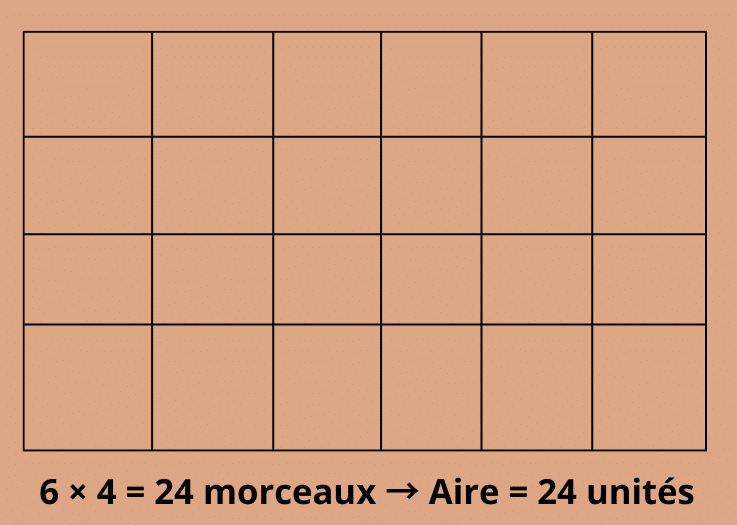
Exemple 1 : La tablette de chocolat
Une tablette de chocolat a 6 carrés de long et 4 carrés de large. Combien de carrés contient-elle ?
Aire = 6 × 4 = 24 carrés
La tablette contient donc 24 petits morceaux de chocolat.
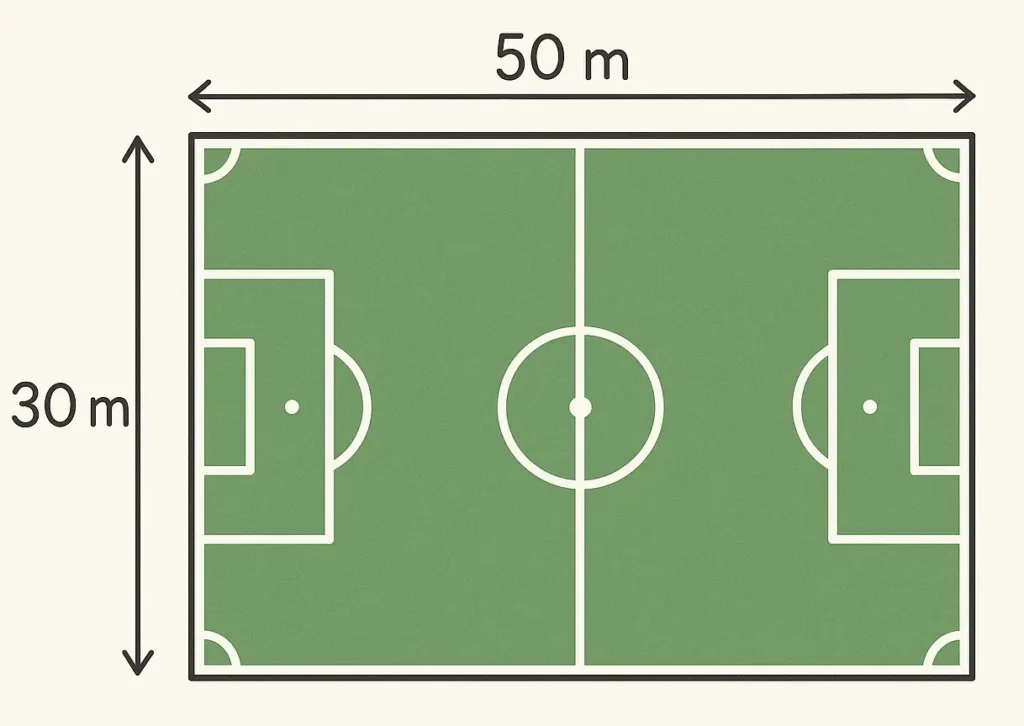
Exemple 2 : Le terrain de football
Un petit terrain mesure 50 m de long et 30 m de large. Quelle est son aire ?
Aire = 50 × 30 = 1 500 m²
Le terrain occupe donc 1 500 mètres carrés, comme si on le recouvrait avec 1 500 dalles de 1 m².
Exemple 3 : Le tapis du salon
Un tapis mesure 2,5 m de long et 1,2 m de large. Quelle est son aire ?
Aire = 2,5 × 1,2 = 3 m²
Le tapis couvre donc 3 mètres carrés de sol.
Astuce : pour bien mémoriser la formule, pense toujours à la phrase : L’aire d’un rectangle, c’est longueur fois largeur.
À Quoi Sert le Calcul d’Aire dans la Vie Quotidienne ?
Savoir calculer l’aire d’un rectangle n’est pas seulement un exercice de maths à l’école, c’est une compétence utile au quotidien.
- Pour savoir si un tapis recouvrira bien le sol du salon.
- Pour mesurer la surface d’un jardin avant d’acheter du gazon.
- Pour comparer deux écrans de tablette et voir lequel est vraiment plus grand.
- Pour calculer combien de pièces de LEGO ou de puzzles entrent dans une base rectangulaire.
Ces exemples montrent que l’aire est une mesure concrète, présente dans de nombreuses situations de la vie de tous les jours.
Exercices Corrigés sur l’Aire du Rectangle
Exercice 1 :
Un rectangle mesure 9 cm de long et 7 cm de large.
Aire = 9 × 7 = 63 cm²
Exercice 2 :
Un terrain rectangulaire mesure 20 m × 15 m.
Aire = 20 × 15 = 300 m²
Exercice 3 :
Un rectangle mesure 4,5 cm × 2,5 cm.
Aire = 4,5 × 2,5 = 11,25 cm²
Exercice 4 :
Une table mesure 120 cm × 80 cm.
Aire = 120 × 80 = 9 600 cm² = 0,96 m²
Exercice 5 :
Un tapis mesure 3,2 m × 2,4 m.
Aire = 3,2 × 2,4 = 7,68 m²
Conclusion : Tu es maintenant un Expert de l’Aire
Tu sais maintenant comment calculer l’aire d’un rectangle.
Deux méthodes existent :
- Compter les petits carreaux pour comprendre le concept.
- Utiliser la formule Aire = Longueur × Largeur pour aller plus vite.
L’aire se mesure toujours en unités carrées (cm², m²). Elle représente la surface à l’intérieur du rectangle et non son contour.
Avec de l’entraînement, tu pourras calculer l’aire de n’importe quel objet rectangulaire de la vie quotidienne : cahier, table, tapis ou terrain de sport.
Gardez ce Guide et Aidez les Autres !
Si cet article t’a aidé, la meilleure façon de le conserver est de l’épingler sur Pinterest ! Tu pourras le retrouver facilement et aideras d’autres élèves à comprendre. Chaque partage est un vrai soutien !
Questions Fréquentes sur le Calcul de l’Aire
Et si la forme n’est pas un rectangle ?
On ne peut pas utiliser directement la formule. Pour un carré, c’est côté × côté. Pour les triangles ou les cercles, il existe d’autres formules adaptées.
Que se passe-t-il si les mesures ne sont pas en carreaux mais en centimètres (cm) ?
On mesure avec une règle et on applique la formule. Exemple : 8 cm × 5 cm = 40 cm².
Pourquoi l’aire se mesure en carrés (cm², m²) ?
Parce qu’on recouvre la surface avec des petits carrés de mesure 1 cm ou 1 m de côté.
Est-ce que l’aire et le périmètre, c’est la même chose ?
Non. Le périmètre mesure le contour, l’aire mesure l’espace à l’intérieur.
Comment calculer l’aire d’un rectangle avec des nombres décimaux ?
La formule reste la même. Exemple : 2,5 m × 1,2 m = 3 m².
Quelle est la différence entre aire et surface ?
Ces mots désignent la même chose en mathématiques. L’aire est une mesure chiffrée de la surface.
