comprendre les mesures en mathématiques
Les mesures font partie des apprentissages essentiels en mathématiques, car elles permettent de relier les notions étudiées à la vie quotidienne : mesurer une distance, peser un aliment, calculer une surface ou encore connaître la capacité d’un support numérique.
Dans cet exercice mathématique mesure, l’élève découvre plusieurs types de grandeurs :
- la longueur, pour mesurer une distance ;
- la masse, pour peser un objet ;
- l’aire, pour comparer des surfaces ;
- et la capacité de stockage numérique, utilisée pour les fichiers informatiques.
L’objectif de ce cours est de rendre les conversions entre unités simples et visuelles, grâce à une méthode claire : le tableau de conversion. Cette méthode permet d’éviter les erreurs fréquentes liées aux multiplications ou divisions par 10, 100 ou 1000À la fin de la leçon, les élèves sauront utiliser le même raisonnement pour toutes les mesures :
Il suffit de placer les chiffres du nombre dans le tableau jusqu’à l’unité demandée.
Table of Contents
Table of Contents
Mesure des longueurs
Rappel des unités
La mesure des longueurs sert à évaluer une distance.
L’unité principale est le mètre (m).
Ses multiples et sous-multiples sont les suivants :
1 km = 1000 m
1 m = 100 cm
1 cm = 10 mm
Méthode avec le tableau de conversion
Pour réussir un exercice mathématique de mesure, il n’est pas nécessaire de diviser ni de multiplier.
La méthode du tableau de conversion est plus simple et plus visuelle.
Voici les étapes à suivre :
Écrire le chiffre des unités du nombre dans la colonne correspondant à l’unité de départ.
Remplir les colonnes vers la droite si on veut une plus petite unité, ou vers la gauche si on veut une plus grande unité.
Chaque colonne doit contenir un seul chiffre.
Cette méthode permet de visualiser clairement la conversion et d’éviter les erreurs de sens.
Exemple
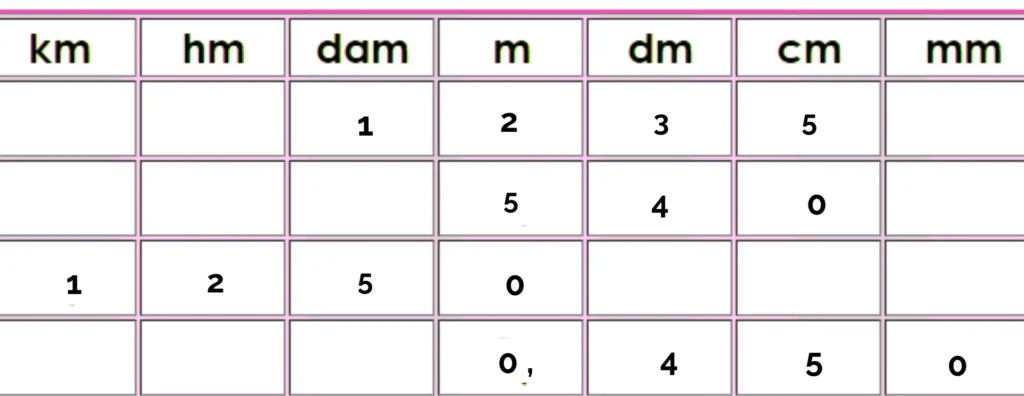
Convertissons 12,35 m en cm :
Le 5 est placé dans la colonne des millimètres, car il correspond à la partie décimale du nombre.
On lit donc :
12,35 m = 1235 cm
Mesure des masses
Rappel des unités
La masse permet de mesurer la quantité de matière contenue dans un objet.
L’unité principale est le gramme (g).
Ses multiples et sous-multiples sont les suivants :
Méthode avec le tableau de conversion
Pour réussir un exercice mathématique de mesure, on utilise le tableau de conversion.
Il permet de visualiser facilement la relation entre les unités, sans faire de calculs complexes.
Voici les étapes à suivre :
Écrire le chiffre des unités du nombre dans la colonne correspondant à l’unité de départ.
Compléter les colonnes jusqu’à l’unité demandée.
S’il manque des chiffres, on met des zéros.
Chaque colonne doit contenir un seul chiffre.
Exemple
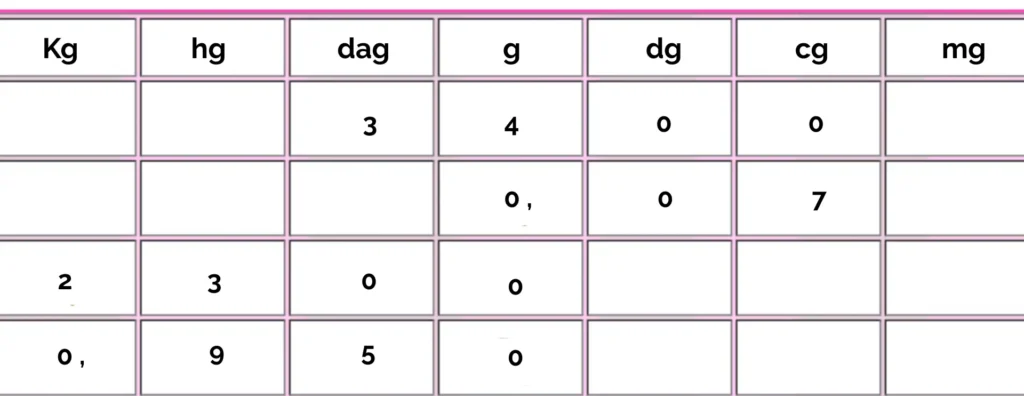
Convertissons 34 g en cg :
On lit :
34 g = 3 400 cg
Autre exemple : 7 cg → g
On lit :
7 cg = 0,07 g
Mini-exercice
Complète les conversions suivantes :
2,3 kg → …… g
950 g → …… kg
250 cg → …… g
Corrigé :
2 300 g
0,95 kg
2,5 g
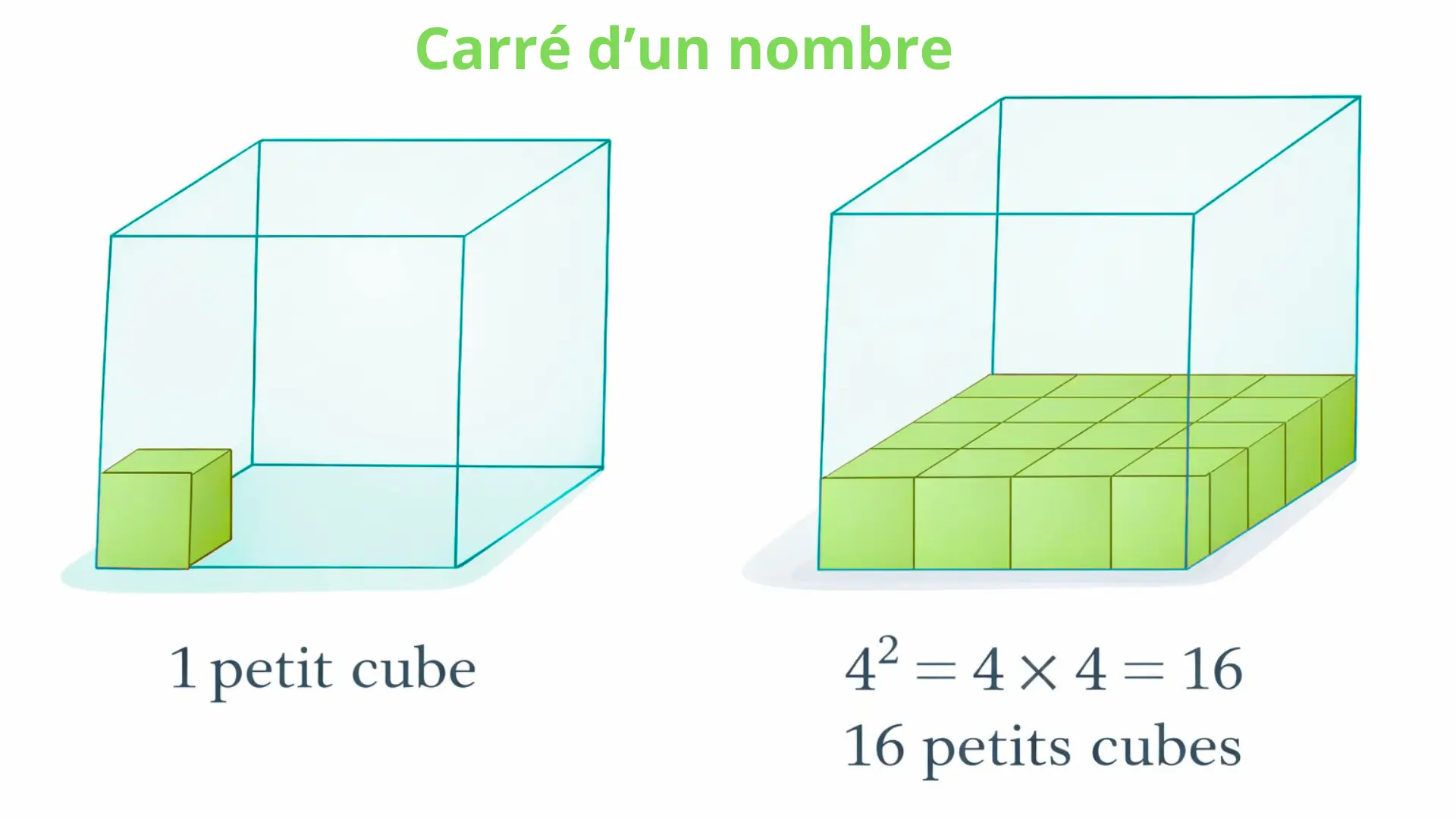
Mesure des aires
Rappel des unités
La mesure des aires permet de déterminer la surface d’une figure.
L’unité principale est le mètre carré (m²).
Ses multiples et sous-multiples sont :
- 1 m² = 100 dm²
- 1 dm² = 100 cm²
- 1 cm² = 100 mm²
Chaque passage d’une unité à la suivante se fait donc en multipliant ou divisant par 100, car une surface a deux dimensions (longueur et largeur).
Mais grâce au tableau de conversion, il n’est pas nécessaire de faire ces calculs : il suffit de placer correctement les chiffres dans les bonnes colonnes.
Méthode avec le tableau de conversion
Pour chaque exercice mathématique de mesure, on utilise la même logique :
On écrit le chiffre des unités dans la colonne correspondant à l’unité de départ.
On avance ou recule dans le tableau deux colonnes par rang, puisque les aires ont deux dimensions.
On complète les colonnes vides avec des zéros si nécessaire.
On lit le résultat à partir de la colonne de l’unité demandée.
Exemple
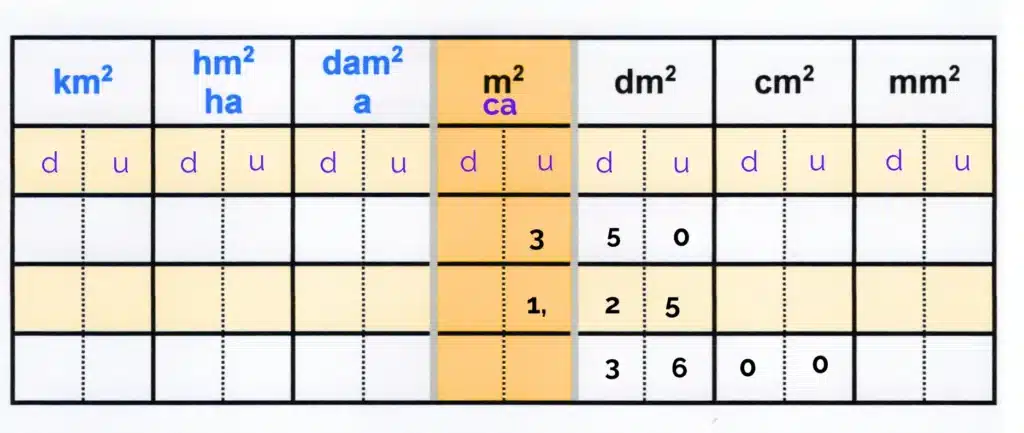
Convertissons 4,5 m² en cm² :
On lit :
4,5 m² = 45 000 cm²Autre exemple : 12 000 cm² → m²
On lit :
12 000 cm² = 1,2 m²
On lit :
12 000 cm² = 1,2 m²
Mini-exercice
Complète ces conversions :
3,5 m² → …… dm²
125 dm² → …… m²
0,36 m² → …… cm²
Corrigé :
350 dm²
1,25 m²
3 600 cm²
Mesure de la capacité de stockage numérique
Rappel des unités
La mesure de la capacité de stockage numérique sert à indiquer la quantité d’informations qu’un support (ordinateur, clé USB, téléphone, carte mémoire, etc.) peut contenir. L’unité principale est le octet (O).
Voici les unités les plus courantes utilisées en informatique :
- 1 Go = 1 000 Mo
- 1 Mo = 1 000 Ko
- 1 Ko = 1 000 octets
Chaque passage d’une unité à la suivante correspond donc à trois colonnes dans le tableau (car on multiplie ou on divise par 1000).
Méthode avec le tableau de conversion
Comme pour les autres grandeurs, la méthode du tableau de conversion reste la même.
C’est la manière la plus claire d’apprendre à faire les conversions dans un exercice mathématique de mesure.
Écrire le chiffre des unités dans la colonne correspondant à l’unité de départ.
Compléter les colonnes jusqu’à l’unité demandée.
Remplir les cases vides avec des zéros. Lire le résultat à partir de la colonne de l’unité d’arrivée.
Exemple
Convertissons 1 Go en Mo
On lit :
1 Go = 1 000 Mo
Autre exemple : 451,9 Go → Mo
On lit :
451,9 Go = 451 900 Mo
Le cas particulier du bit et de l’octet
Avant de terminer cette leçon, il est important de comprendre la plus petite unité utilisée en informatique : le bit (b).
- 1 octet (O) = 8 bits (b)
- Le bit sert à représenter une seule information : 0 ou 1.
- L’octet regroupe 8 bits pour former une donnée plus complète (une lettre, un chiffre ou un symbole).
Exemples :
- 12 octets = 96 bits
- 80 bits = 10 octets
Mini- exercice
Complète ces conversions :
2 500 Mo → …… Go
3 Go → …… Mo
9 octets → …… bits
Corrigé :
2,5 Go
3 000 Mo
72 bits
Exercices de révision
Ces exercices de mesure permettent de s’entraîner à utiliser le tableau de conversion pour toutes les grandeurs : longueurs, masses, aires et capacités de stockage numérique.
Ils aident l’élève à consolider la méthode et à éviter les erreurs de sens ou de position des chiffres.
A. Mesure des longueurs
5,4 m → …… cm
720 cm → …… m
1,25 km → …… m
450 mm → …… m
0,82 dam → …… cm
Corrigé :
540 cm
7,2 m
1 250 m
0,45 m
820 cm
B. Mesure des masses
2,3 kg → …… g
950 g → …… kg
25 dg → …… g
7 cg → …… g
4,2 g → …… mg
Corrigé :
2 300 g
0,95 kg
2,5 g
0,07 g
4 200 mg
C. Mesure des aires
3,5 m² → …… dm²
125 dm² → …… m²
0,36 m² → …… cm²
2 400 cm² → …… m²
5,2 dm² → …… cm²

Corrigé :
350 dm²
1,25 m²
3 600 cm²
0,24 m²
520 cm²
D. Mesure de la capacité de stockage numérique
2 500 Mo → …… Go
3 Go → …… Mo
5 000 Ko → …… Mo
8 octets → …… bits
80 bits → …… octets
Corrigé :
2,5 Go
3 000 Mo
5 Mo
64 bits
10 octets
Ces exercices sont conçus pour que chaque élève puisse s’exercer à son rythme.
L’enseignant peut les proposer en classe, à la maison ou les intégrer dans une fiche PDF d’entraînement.
Conseils pour réussir les exercices
Au fil de mon expérience d’enseignante, j’ai remarqué que les élèves rencontrent souvent les mêmes difficultés lorsqu’ils effectuent un exercice mathématique de mesure.
Les erreurs ne viennent pas d’un manque de compréhension, mais plutôt d’un manque d’attention à certaines étapes importantes.
Voici quelques conseils pratiques pour progresser :
- Toujours identifier l’unité de départ et celle d’arrivée.
Avant de commencer, encadre ces deux unités dans ton tableau. Cela t’aidera à savoir dans quelle colonne placer les chiffres. - Écrire le chiffre des unités à la bonne place.
Beaucoup d’élèves font des erreurs en écrivant le premier chiffre au mauvais endroit.
Rappelle-toi : le chiffre des unités du nombre de départ doit toujours être placé dans la colonne correspondant à cette unité. - Ne saute aucune colonne.
Lorsque tu passes d’une unité à une autre, avance ou recule colonne par colonne.
Chaque colonne représente une étape de conversion. - Ne jamais mélanger les unités.
Parfois, les élèves confondent mètres et grammes, ou cm² et cm.
Pense toujours à vérifier si tu mesures une longueur, une masse, une surface ou une capacité de stockage numérique. - Pour les nombres décimaux, place la virgule avec soin.
C’est souvent la plus grande source d’erreurs : la virgule change de place selon les colonnes.
Si tu hésites, refais ton tableau et vérifie que tu as bien rempli chaque case avant de lire le résultat. - Vérifie la cohérence du résultat.
Si tu convertis dans une unité plus petite (par exemple de m en cm), ton résultat doit être un nombre plus grand.
Si tu vas vers une unité plus grande (de g vers kg), ton résultat doit être plus petit. - Utilise toujours le tableau, même pour les petites conversions.
C’est le moyen le plus sûr d’éviter les erreurs, surtout quand on débute.
Ces conseils simples permettent à chaque élève de gagner en autonomie et de réussir les conversions sans confusion.
Ils sont également très utiles pour les parents et enseignants qui accompagnent les enfants dans leurs apprentissages.
Conclusion
Ce cours sur la mesure en mathématiques t’a permis de revoir les principales grandeurs : longueur, masse, aire et capacité de stockage numérique.
Grâce à la méthode du tableau de conversion, chaque élève peut désormais réussir ses exercices sans confusion ni calculs compliqués.
Le secret de la réussite est simple :
- Placer les chiffres dans les bonnes colonnes,
- Vérifier l’unité de départ et d’arrivée,
- Et relire le résultat pour s’assurer qu’il est logique.
En suivant cette méthode, les conversions deviennent faciles et automatiques.
En tant qu’enseignante, j’ai remarqué que cette approche visuelle aide les élèves à progresser rapidement, même ceux qui avaient des difficultés au départ. Pour aller plus loin, télécharge la fiche PDF d’exercices proposée à la fin de cet article.
Elle contient plusieurs activités illustrées à imprimer pour t’entraîner à ton rythme, seul(e) ou en classe.
Ces visuels te permettront de revoir la leçon en un coup d’œil, de t’entraîner à la maison ou de les partager avec tes camarades. Continue à explorer CoursCool.com pour découvrir d’autres leçons illustrées et des fiches à télécharger.
Et si tu veux progresser encore plus vite, suis moi sur Pinterest pour ne manquer aucun nouveau contenu !
Foire aux questions (FAQ)
Pourquoi faut-il apprendre à convertir les unités de mesure ?
Apprendre à convertir les unités aide à mieux comprendre le monde qui nous entoure : mesurer une distance, calculer une surface, peser un objet ou encore connaître la capacité d’un appareil numérique.
Les conversions sont utilisées dans la vie quotidienne, en science, en technologie et même en cuisine.
Quelle est la méthode la plus simple pour faire une conversion ?
La méthode la plus simple est celle du tableau de conversion.
Il suffit d’écrire le chiffre des unités du nombre dans la colonne correspondant à l’unité de départ, puis de remplir les colonnes jusqu’à celle de l’unité d’arrivée.
Chaque colonne ne contient qu’un seul chiffre, ce qui évite les erreurs de calcul.
Pourquoi certains élèves se trompent dans les conversions ?
Les erreurs les plus fréquentes viennent d’un mauvais placement des chiffres dans le tableau ou d’une mauvaise lecture de l’unité demandée.
Certains élèves oublient aussi de placer correctement la virgule.
Avec un peu d’entraînement, ces erreurs disparaissent rapidement.
Quelle est la différence entre les unités de longueur, de masse, d’aire et de stockage numérique ?
Les longueurs servent à mesurer des distances.
Les masses servent à mesurer le poids des objets.
Les aires permettent de mesurer des surfaces.
Les unités de stockage numérique indiquent la quantité d’informations que peut contenir un appareil informatique.
Quelle est la relation entre le bit et l’octet ?
Le bit est la plus petite unité utilisée en informatique.
Un octet regroupe 8 bits.
Par exemple :
1 octet = 8 bits
10 octets = 80 bits
Cette conversion est très fréquente dans les exercices sur la mesure de la capacité de stockage numérique.
Comment aider un élève à progresser dans les conversions ?
L’idéal est de travailler régulièrement avec le tableau de conversion.
L’enfant doit comprendre le sens du passage d’une unité à une autre et s’entraîner avec des exemples concrets.
Les exercices proposés dans cet article sont conçus pour cela : ils suivent une progression simple et logique.