Exercices nombres décimaux 6e (avec rappel de cours et fiche à imprimer)

Les Exercices nombres décimaux 6e sont souvent une étape délicate pour les élèves, car la virgule peut sembler mystérieuse au début : on confond la partie entière et la partie décimale, on hésite sur la lecture, et les comparaisons deviennent vite confuses. C’est normal : les nombres décimaux demandent un peu de pratique et surtout des explications concrètes.

Cette fiche a été conçue pour expliquer simplement chaque notion : lecture, comparaison, placement sur une droite graduée, encadrement, addition et soustraction. Chaque partie propose un rappel court, des erreurs fréquentes expliquées, des astuces faciles à retenir, et des exercices progressifs pour consolider les apprentissages.

Si toi (ou ton enfant) rencontres des difficultés à comprendre une partie de la leçon, je serai ravie de répondre à vos questions ou d’expliquer à nouveau ce qui pose problème. Vous pouvez m’écrire directement via le site CoursCool.com ou sur Pinterest – CoursCool, où je partage aussi d’autres fiches et activités à imprimer.

À la fin de cette page, tu trouveras une fiche PDF complète à télécharger, prête à utiliser en classe ou à la maison.

Lire et écrire les nombres décimaux

Objectif

Savoir lire, écrire et décomposer un nombre décimal en distinguant la partie entière et la partie décimale.

Rappel du cours

Un nombre décimal contient une virgule.

• La partie avant la virgule s’appelle la partie entière.
• La partie après la virgule s’appelle la partie décimale.

Exemple : 24,7 se lit vingt-quatre virgule sept.
Partie entière : 24
Partie décimale : 7
Ce nombre représente 24 unités et 7 dixièmes.

Autre exemple : 3,45 = 3 unités + 4 dixièmes + 5 centièmes.

Tableau de numération :

Erreur fréquente

Certains élèves lisent 3,45 comme “trois quarante-cinq” au lieu de “trois virgule quarante-cinq”.

Astuce du prof

Pense à dire “virgule” comme une pause dans la lecture. Lis séparément la partie entière et la partie décimale.

Exercices

1. Lis correctement ces nombres : 2,5 – 7,35 – 12,08 – 0,9
2. Écris en lettres : 5,2 – 8,45 – 0,3 – 14,07
3. Décompose :
   a) 4,3 = … unités + … dixièmes
   b) 7,24 = … unités + … dixièmes + … centièmes

Comparer et ranger les nombres décimaux

Objectif

Savoir comparer deux ou plusieurs nombres décimaux en observant chaque chiffre après la virgule, rang par rang.

Rappel du cours

Pour comparer des nombres décimaux, on procède de gauche à droite :

1. On compare les parties entières.
2. Si elles sont identiques, on compare les dixièmes.
3. Puis les centièmes, et ainsi de suite.

Exemples :

• 3,45 < 3,5 car 4 dixièmes < 5 dixièmes.
• 4,08 < 4,1 car 0 dixième < 1 dixième.
• 7,36 > 7,29 car 3 dixièmes > 2 dixièmes.

Pour ranger plusieurs nombres, on peut les aligner à la virgule et comparer colonne par colonne, sans modifier les nombres.

Erreur fréquente

Certains élèves comparent les chiffres sans tenir compte de leur rang. Par exemple, ils pensent que 3,45 > 3,5 car “45 est plus grand que 5”.

Astuce du prof

Lis chaque nombre en précisant le rang du chiffre : “3 unités et 4 dixièmes” / “3 unités et 5 dixièmes”.

Exercices

1. Indique le signe <, > ou = :
   a) 4,2 ………………. 4,15
   b) 2,35 ………………. 2,4
   c) 5,08 ………………. 5,8
   d) 3,07 ………………. 3,7
2. Range dans l’ordre croissant :
   a) 6,4 – 6,35 – 6,45 – 6,3
   b) 1,08 – 1,8 – 1,75 – 1,005
3. Range dans l’ordre décroissant :
   a) 0,9 – 0,95 – 0,87 – 0,8
   b) 7,5 – 7,45 – 7,55 – 7,505

Placer un nombre décimal sur une droite graduée

Objectif

Savoir placer un nombre décimal sur une droite graduée pour comprendre sa position entre deux entiers.

Rappel du cours

Entre deux entiers consécutifs, on peut diviser l’intervalle en 10 parties égales : chaque graduation représente un dixième.

On peut aussi partager chaque dixième en 10 centièmes pour plus de précision.

Exemples :

Sur une droite de 2 à 3 :

• 2,1 est sur la première graduation après 2.
• 2,5 est au milieu.
• 2,9 est juste avant 3.

Sur une droite de 4 à 5 :

• 4,25 est entre 4,2 et 4,3.
• 4,7 est plus proche de 5.

Placer un nombre aide à visualiser l’encadrement : on voit qu’il se situe entre deux valeurs.

Erreur fréquente

Les élèves placent les nombres “à l’œil” sans respecter les intervalles égaux.

Astuce du prof

Trace d’abord les entiers, puis divise chaque intervalle en dix parties égales. Compte les dixièmes à partir de l’entier de départ.

Exercices

1. Trace une droite de 0 à 2 et place : 0,5 – 1,2 – 1,7 – 1,9.
2. Sur une droite de 3 à 4, place : 3,1 – 3,4 – 3,6 – 3,9.
3. Sur une droite de 5 à 6 :
   a) Quel nombre est au milieu ?
   b) Quel nombre est juste avant 5,4 ?
   c) Quel nombre est juste après 5,8 ?

Encadrer et approcher un nombre décimal

Objectif

Savoir repérer entre quels nombres se situe un nombre décimal et donner une valeur proche (arrondie).

Rappel du cours

Encadrer un nombre décimal, c’est indiquer deux nombres entre lesquels il se trouve.

Exemples :

• 3,45 est entre 3 et 4 (à l’unité près)
• 3,45 est entre 3,4 et 3,5 (au dixième près)
• 3,45 est entre 3,44 et 3,46 (au centième près)

Approcher un nombre (arrondir), c’est donner une seule valeur proche.
Exemples :

• 4,36 ≈ 4,4
• 2,42 ≈ 2,4

Erreur fréquente

Les élèves confondent encadrer (deux nombres) et arrondir (un seul nombre).

Astuce du prof

Souviens-toi : deux nombres = encadrement, un seul avec ≈ = arrondi.

Exercices

1. Encadre à l’unité près : 2,7 – 4,3 – 6,85 – 0,9
2. Encadre au dixième près : 3,45 – 7,62 – 8,09 – 12,73
3. Arrondis au dixième : 9,46 – 5,82 – 2,38 – 10,14

Addition et soustraction de nombres décimaux

Objectif

Savoir poser et effectuer correctement une addition ou une soustraction avec des nombres décimaux.

Rappel du cours

On aligne toujours les virgules avant de calculer.

Chaque chiffre doit être dans la même colonne : unités avec unités, dixièmes avec dixièmes.

Exemples :

Addition

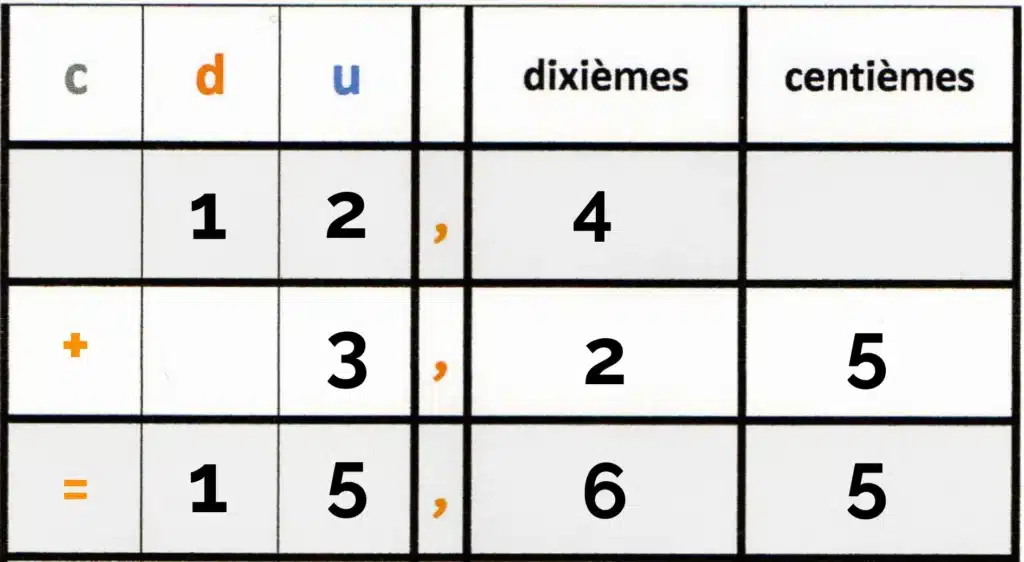
Soustraction

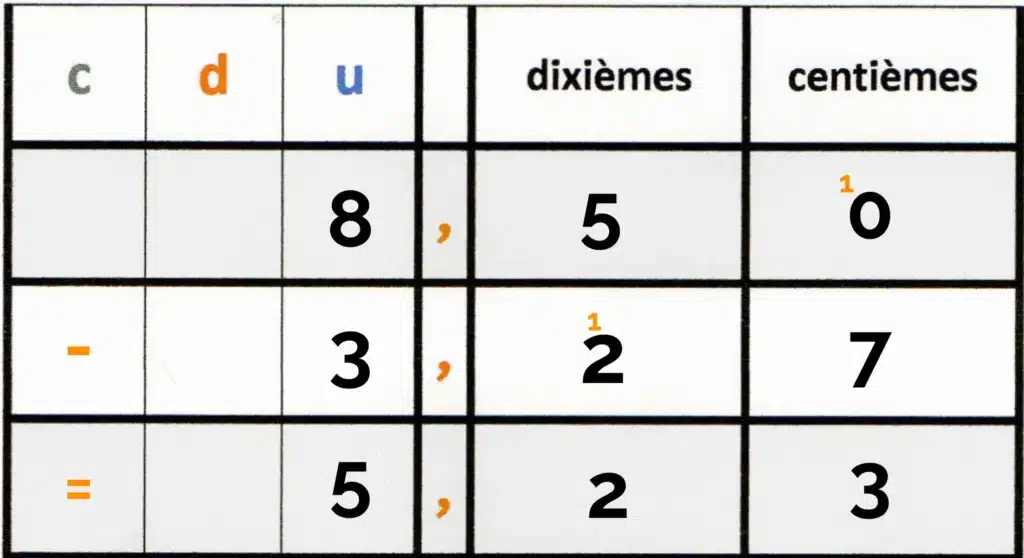
Erreur fréquente

Certains élèves alignent les chiffres à droite sans tenir compte des virgules.

Astuce du prof

Avant de calculer, vérifie que toutes les virgules forment une colonne droite.

Exercices

1. Additions : 4,5 + 2,35 ; 7,2 + 0,85 ; 12,4 + 3,25 ; 9,05 + 0,7
2. Soustractions : 8,5 − 3,27 ; 6,42 − 1,8 ; 10,3 − 9,75 ;7,25 − 4,5
3. Problèmes :
   a) Léa achète un livre à 4,75 € et un cahier à 2,3 €. Combien dépense-t-elle ?
   b) Un mètre de tissu coûte 7,8 €. On enlève 3,45 €. Combien reste-t-il à payer ?
   c) Tom mesure 1,45 m et Paul 1,38 m. Quelle est la différence de taille ?

Relier nombres décimaux et fractions

Objectif

Comprendre que les nombres décimaux représentent les mêmes valeurs que certaines fractions.

Rappel du cours

Chaque chiffre après la virgule indique une partie de l’unité :

• 0,1 = 1/10
• 0,5 = 5/10 = 1/2
• 0,25 = 25/100 = 1/4
• 0,75 = 75/100 = 3/4

Erreur fréquente

Certains pensent que la virgule sépare deux nombres, alors qu’elle indique une fraction de l’unité.

Astuce du prof

Utilise des exemples concrets :

• 0,5 L = un demi-litre
• 0,25 m = un quart de mètre
• 0,1 € = un dixième d’euro

Exercices

1. Complète : 0,1 = …/10 ; 0,3 = …/10 ; 0,25 = …/100 ; 0,75 = …/100
2. Écris sous forme décimale : 1/10 = … ; 5/10 = … ; 25/100 = … ; 3/4 = …
3. Relie les équivalences :
   1/2 – 0,5 ; 1/4 – 0,25 ; 3/4 – 0,75

Conclusion

Les nombres décimaux sont partout dans la vie quotidienne : sur les prix, les mesures, les distances ou les notes.

C’est pourquoi il est essentiel, en CM2, de savoir les lire, les comparer, les encadrer et les utiliser dans des calculs.

Pour réviser, télécharge la fiche PDF complète Exercices nombres décimaux 6e : elle contient le cours, les exercices et le corrigé.

Retrouve aussi d’autres fiches et idées d’activités sur Pinterest .

Mot du prof

Si tu trouves certaines parties difficiles à comprendre ou si tu veux que j’explique une autre leçon, écris- moi directement via le site ou sur Pinterest

CoursCool.

Je lis tous les messages et j’adapte les prochaines fiches selon vos besoins.

Souviens- toi : comprendre les décimaux, c’est observer, réfléchir et oser poser des questions. Chaque progrès compte !

FAQ : Exercices nombres décimaux 6e