La fiche d’exercices sur les fractions multiplication et division présente deux opérations essentielles en mathématiques dès le CM2 et la 6e. Ces notions permettent de résoudre des problèmes de proportionnalité, de partage et de calculs dans de nombreuses situations quotidiennes. Grâce à cette fiche, l’élève peut comprendre les règles, suivre des exemples simples et s’entraîner avec des exercices progressifs et adaptés à son niveau.
Les activités proposées conviennent aussi bien aux élèves qu’aux enseignants et aux parents qui souhaitent réviser cette notion de manière claire et structurée. Une fiche PDF complète est disponible à la fin de l’article pour continuer à s’exercer en autonomie.
Table of Contents
Rappel : Qu’est-ce qu’une fraction ?
Une fraction sert à représenter une partie d’un tout ou une division entre deux nombres. Elle permet de décrire des quantités qui ne sont pas entières, comme un demi-gâteau, un quart de litre ou trois quarts d’une longueur.
Une fraction est écrite sous la forme numérateur / dénominateur :
- Le numérateur (en haut) indique combien de parts sont prises.
- Le dénominateur (en bas) indique en combien de parts égales le tout est partagé.
Exemple :
Dans 3/4, le tout est partagé en 4 parts égales et on en prend 3.
Fractions équivalentes
Deux fractions sont dites équivalentes lorsqu’elles représentent la même quantité, même si leurs nombres sont différents.
Exemples :
- 1/2 = 2/4 = 3/6
- 1/3 = 2/6
On obtient une fraction équivalente en multipliant ou en divisant le numérateur et le dénominateur par le même nombre.
Simplification d’une fraction
Simplifier une fraction consiste à réduire les deux nombres (numérateur et dénominateur) en divisant par le même nombre, pour obtenir une fraction plus simple.
Exemples :
- 6/8 → diviser par 2 → 3/4
- 10/15 → diviser par 5 → 2/3
La simplification est très utile pour la multiplication et la division des fractions.
Multiplier deux fractions
Multiplier deux fractions est une opération simple lorsque l’on connaît la règle. Contrairement à l’addition ou à la soustraction, il n’est pas nécessaire d’avoir le même dénominateur. On peut multiplier directement les deux numérateurs entre eux, puis les deux dénominateurs entre eux.
C’est une opération très utilisée en proportionnalité, en géométrie (aires), et dans certains problèmes du quotidien.
Règle de multiplication (CM2–6e)
Pour multiplier deux fractions :
- On multiplie les numérateurs entre eux.
- On multiplie les dénominateurs entre eux.
- On simplifie la fraction obtenue si possible.
Forme générale :
(numérateur × numérateur) / (dénominateur × dénominateur)
Exemple simple (niveau CM2)
Calculer : 2/3 × 1/4
Étapes :
- Multiplier les numérateurs : 2 × 1 = 2
- Multiplier les dénominateurs : 3 × 4 = 12
Résultat : 2/12
Simplification : 2/12 = 1/6
Exemple plus avancé (niveau 6e)
Calculer : 3/5 × 4/7
Étapes :
- Numérateurs : 3 × 4 = 12
- Dénominateurs : 5 × 7 = 35
Résultat : 12/35
Cette fraction ne peut pas être simplifiée.

Peut-on simplifier avant de multiplier ?
Oui, c’est possible et même conseillé en 6e.
Exemple :
4/9 × 3/8
Avant de multiplier :
- 4 et 8 sont divisibles par 4 → 4/8 devient 1/2
- 3 et 9 sont divisibles par 3 → 3/9 devient 1/3
Nouveau calcul :
1/3 × 1/2 = 1/6
Cette technique évite de manipuler de grands nombres.
Erreurs fréquentes à éviter
- Mélanger multiplication et addition (ex : 2/3 + 1/4).
- Multiplier les dénominateurs mais additionner les numérateurs.
- Oublier de simplifier le résultat.
- Oublier que les dénominateurs n’ont pas besoin d’être identiques.
Division de fractions
Diviser deux fractions peut sembler difficile au premier abord, mais il suffit de connaître une seule règle : diviser par une fraction revient à multiplier par son inverse.
Cette méthode simplifie beaucoup les calculs et permet d’obtenir rapidement le résultat.
Règle : multiplier par l’inverse
Pour diviser une fraction par une autre :
- On garde la première fraction telle qu’elle est.
- On inverse la deuxième fraction (le numérateur devient dénominateur et inversement).
- On multiplie les deux fractions.
- On simplifie si possible.
Exemple d’inverse :
- L’inverse de 2/3 est 3/2.
- L’inverse de 5/8 est 8/5.
Exemple simple (niveau CM2)
Calculer : 3/4 ÷ 1/2
Étapes :
- Garder 3/4
- Inverser 1/2 → 2/1
- Multiplier :
3/4 × 2/1 = 6/4 - Simplifier : 6/4 = 3/2
Exemple plus avancé (niveau 6e)
Calculer : 5/6 ÷ 2/3
Étapes :
- Garder 5/6
- Inverser 2/3 → 3/2
- Multiplier :
5/6 × 3/2 = 15/12 - Simplifier :
15/12 → diviser par 3 → 5/4

Exemple avec simplification avant multiplication
Calculer : 4/9 ÷ 3/5
Étapes :
- Garder 4/9
- Inverser 3/5 → 5/3
- Simplifier avant d’effectuer le calcul :
- 4 et 3 n’ont rien en commun
- 5 et 9 n’ont rien en commun
Donc on multiplie directement.
- Multiplier :
4/9 × 5/3 = 20/27
Résultat final : 20/27
Erreurs fréquentes à éviter
- Oublier d’inverser la deuxième fraction.
- Inverser la première fraction au lieu de la seconde.
- Confondre division et soustraction.
- Oublier de simplifier le résultat.
- Croire qu’il faut le même dénominateur (comme pour l’addition/soustraction).
Exercices : Multiplier des fractions (CM2)
2/3 × 1/4 =
1/2 × 3/5 =
3/4 × 1/3 =
2/5 × 2/3 =
4/6 × 1/2 =
Exercices : Multiplier des fractions (6e)
5/7 × 3/4 =
4/9 × 2/3 =
7/10 × 5/14 =
3/8 × 4/15 =
6/11 × 5/6 =
Exercices : Diviser des fractions (CM2)
3/4 ÷ 1/2 =
2/3 ÷ 1/3 =
1/5 ÷ 1/10 =
4/6 ÷ 2/3 =
1/8 ÷ 1/4 =
Exercices : Diviser des fractions (6e)
5/6 ÷ 2/3 =
7/9 ÷ 1/3 =
4/7 ÷ 2/5 =
3/10 ÷ 3/4 =
5/12 ÷ 1/6 =
Correction : Multiplication de fractions
2/3 × 1/4 = 2/12 = 1/6
1/2 × 3/5 = 3/10
3/4 × 1/3 = 3/12 = 1/4
2/5 × 2/3 = 4/15
4/6 × 1/2 =
4/6 = 2/3
→ 2/3 × 1/2 = 2/6 = 1/3
5/7 × 3/4 = 15/28
4/9 × 2/3 = 8/27
7/10 × 5/14
7/14 = 1/2
→ 1/2 × 5/10 = 5/20 = 1/4
3/8 × 4/15 =
Simplification : 4/8 → 1/2
→ 3/2 × 1/15 = 3/30 = 1/10
6/11 × 5/6 =
Simplification : 6/6 = 1
→ 5/11
Correction : Division de fractions
3/4 ÷ 1/2 =
3/4 × 2/1 = 6/4 = 3/2
2/3 ÷ 1/3 =
2/3 × 3/1 = 6/3 = 2
1/5 ÷ 1/10 =
1/5 × 10/1 = 10/5 = 2
4/6 ÷ 2/3 =
4/6 = 2/3
2/3 × 3/2 = 6/6 = 1
1/8 ÷ 1/4 =
1/8 × 4/1 = 4/8 = 1/2
5/6 ÷ 2/3 =
5/6 × 3/2 = 15/12 = 5/4
7/9 ÷ 1/3 =
7/9 × 3/1 = 21/9 = 7/3
4/7 ÷ 2/5 =
4/7 × 5/2 = 20/14 = 10/7
3/10 ÷ 3/4 =
3/10 × 4/3
3 simplifie :
→ 1/10 × 4/1 = 4/10 = 2/5
5/12 ÷ 1/6 =
5/12 × 6/1 = 30/12 = 5/2
Conseils pour les enseignants et parents
Accompagner un élève dans la multiplication et la division des fractions nécessite une approche progressive. Les notions restent abstraites si l’élève ne les voit pas et ne comprend pas leur logique. Voici trois stratégies efficaces pour faciliter la compréhension.
Comment expliquer la multiplication ?
Pour expliquer la multiplication de fractions, il est essentiel de partir de l’idée suivante :
Multiplier une fraction revient à prendre une partie d’une partie.
Exemple concret :
« Si je prends 1/2 d’un gâteau, puis encore 1/3 de cette moitié, combien ai-je pris du gâteau entier ? »
→ Cela revient à calculer : 1/2 × 1/3.
Ensuite, présenter la règle de manière très simple :
- On multiplie les nombres du haut.
- On multiplie les nombres du bas.
- On simplifie si possible.
Ce raisonnement fonctionne toujours, et sa régularité aide l’élève à mémoriser la procédure.
Comment expliquer l’inverse ?
Pour comprendre la division, l’élève doit connaître le principe de l’inverse.
L’inverse d’une fraction signifie « retourner la fraction » :
- Le numérateur devient le dénominateur.
- Le dénominateur devient le numérateur.
Exemples :
1/3 → inverse = 3/1
4/5 → inverse = 5/4
Idée à faire retenir :
Diviser par une fraction, c’est multiplier par son inverse.
Exemple concret à expliquer à l’enfant :
« Si je divise une quantité par 1/2, je veux savoir combien de fois un demi tient dans cette quantité. »
Modéliser avec des exemples concrets
La meilleure manière d’enseigner ces notions est de les rendre visibles. Voici quelques méthodes simples :
• Dessins fractionnés
Représenter des rectangles ou des cercles découpés en parts égales permet de montrer :
- la notion de “part de part” pour la multiplication,
- la notion de “combien de fois…” pour la division.
• Bandes ou jetons
Avec des bandes de papier ou des jetons :
- prendre une fraction de la bande,
- puis une fraction de cette fraction (multiplication),
- ou montrer combien de portions de 1/3 on peut faire dans 1 (division).
• Situations de la vie réelle
Quelques exemples utiles :
- Recettes de cuisine (prendre 2/3 d’une quantité)
- Partage de chocolat (combien de fois 1/4 entre dans 1 tablette)
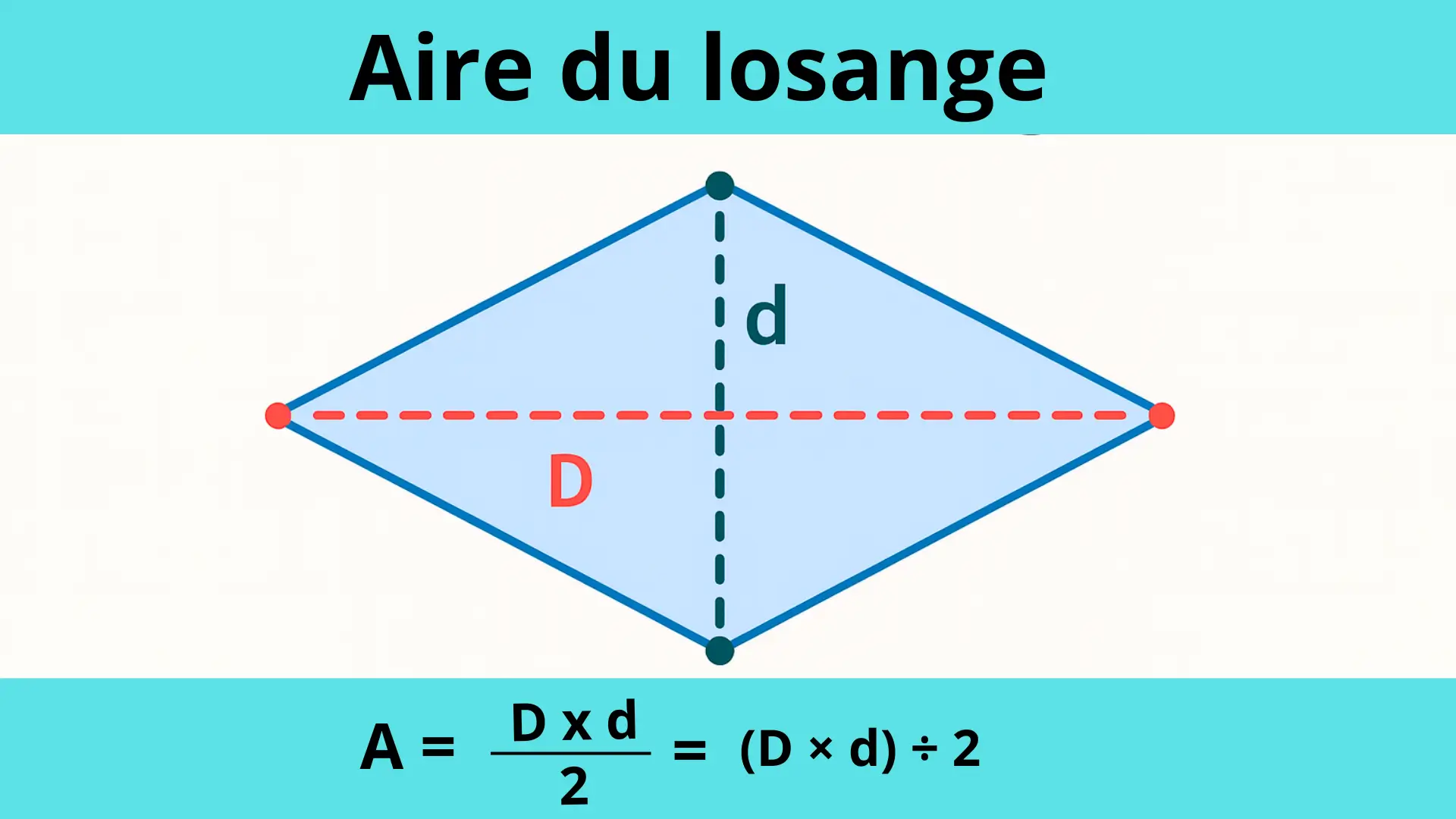
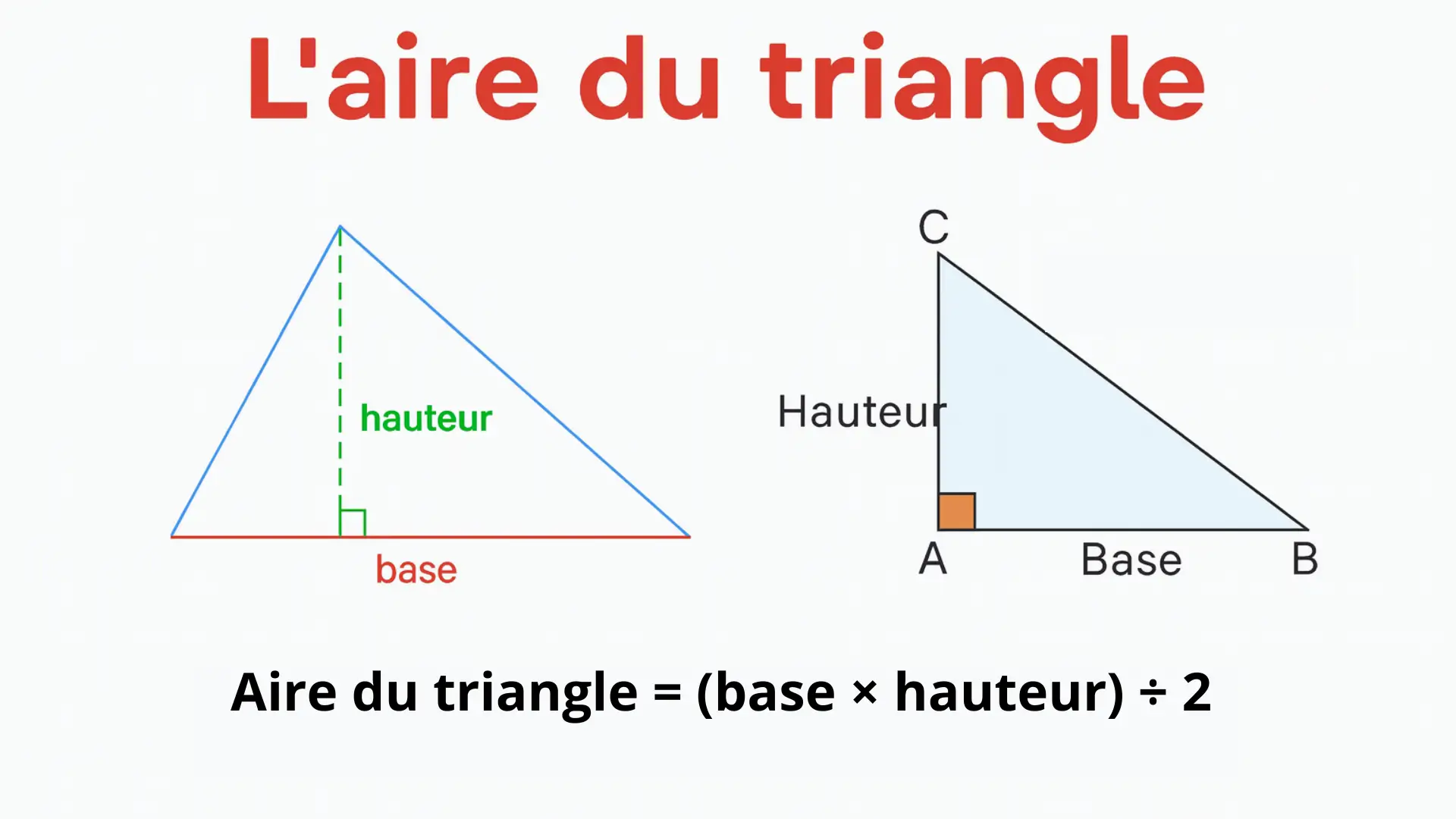
- Aires en géométrie (prendre une fraction d’une proportion)
Lorsque l’élève visualise la situation, les règles apparaissent plus logiques et plus simples à retenir.
Mot du professeur: fractions multiplication et division
Les fractions, la multiplication et la division peuvent sembler difficiles au début, mais chaque étape que tu apprends te rend plus fort en mathématiques. L’important n’est pas d’aller vite, mais de comprendre ce que tu fais et de progresser à ton rythme.
Tu vas peut-être faire des erreurs, et c’est normal. Les erreurs ne sont pas des signes d’échec : ce sont des indices qui montrent ce que tu dois encore travailler. Chaque fois que tu recommences, tu deviens plus confiant et tu comprends mieux.
Continue à t’entraîner, pose des questions quand quelque chose te semble compliqué, et n’oublie jamais que tu es capable de réussir. Tu progresses un peu plus à chaque exercice, même si tu ne le remarques pas tout de suite. Courage, persévère, et tu seras fier de ton travail.
Conclusion
La multiplication et la division des fractions sont des compétences importantes pour progresser en mathématiques à partir du CM2 et tout au long du collège. Comprendre les règles, savoir les appliquer et s’exercer régulièrement permet à l’élève de gagner en assurance et d’aborder les calculs avec plus de facilité.
Les rappels, exemples et activités proposés dans cette fiche offrent une progression simple et efficace pour s’entraîner. Les corrections permettent de vérifier la compréhension et de revenir sur les points difficiles si nécessaire.
Pour aller plus loin, la fiche PDF téléchargeable rassemble l’ensemble des exercices, des règles essentielles et des solutions, afin de réviser à la maison ou en classe en toute autonomie.
Pour découvrir encore plus de fiches de révision en mathématiques, je partage chaque semaine de nouvelles ressources sur Pinterest : exercices, fiches PDF, rappels de leçon et supports visuels adaptés au CM2. Suivez CoursCool sur Pinterest pour accéder à des contenus variés et régulièrement mis à jour, conçus pour aider les élèves à comprendre les notions essentielles avec clarté et confiance.
FAQ : Questions fréquentes
Pourquoi peut-on multiplier les fractions directement ?
Parce que multiplier deux fractions revient à prendre une partie d’une partie.
La règle numérateur × numérateur et dénominateur × dénominateur fonctionne toujours et permet d’obtenir rapidement une nouvelle fraction. Contrairement à l’addition ou la soustraction, il n’est pas nécessaire d’avoir le même dénominateur.
Pourquoi faut-il inverser la deuxième fraction lorsqu’on divise ?
Diviser par une fraction signifie déterminer combien de fois cette fraction tient dans une autre quantité.
L’inversion (prendre l’inverse) permet de transformer cette division en multiplication, ce qui rend le calcul plus simple et plus direct.
Exemple :
1 ÷ 1/2 = 2, car deux fois 1/2 font 1.
L’inversion traduit exactement cette idée.
Que faire si l’élève ne comprend pas l’inverse ?
Revenir aux représentations concrètes est la meilleure méthode.
Par exemple, dessiner une barre de 1 unité et montrer combien de fois 1/3 peut être répété dans cette barre.
Plus l’élève voit la situation, mieux il comprend le principe d’inversion.
Quand faut-il simplifier une fraction ?
Une fraction doit être simplifiée lorsque le numérateur et le dénominateur peuvent être divisés par le même nombre.
Cela rend le résultat plus lisible et aide à mieux voir les relations entre fractions.
Exemples :
6/8 = 3/4
10/15 = 2/3
Pourquoi transforme-t-on parfois les fractions avant de calculer ?
En multiplication, on peut simplifier avant pour éviter de manipuler de grands nombres.
En division, on inverse la deuxième fraction, puis il peut être utile de simplifier avant de multiplier.
La transformation ne change pas le résultat final, elle permet juste de rendre le calcul plus simple et plus rapide.