En géométrie, les angles occupent une place importante au programme de CM2 et de 6e.
Dans ce cours, nous allons étudier la bissectrice d’un angle à travers une explication progressive, des exemples clairs et des exercices corrigés.
Avant de donner directement la définition, nous commencerons par une activité de recherche afin de comprendre concrètement comment fonctionne la bissectrice d’un angle et pourquoi elle partage un angle en deux angles de même mesure.
À la fin de ce cours, tu sauras :
- reconnaître la bissectrice d’un angle,
- construire la bissectrice d’un angle correctement,
- identifier des angles de même mesure,
- comprendre les angles complémentaires et supplémentaires.
Un PDF à télécharger avec le cours et les exercices corrigés est disponible à la fin de l’article.
Table of Contents
Je cherche : découvrir la bissectrice d’un angle
Pour commencer cette leçon sur la bissectrice d’un angle, nous allons réaliser une activité de recherche. Cette activité permet d’observer et de comprendre la notion avant d’en donner la définition.
Trace sur du papier calque un angle AÔB de mesure 60° tel que OA = OB = 5 cm.
Plie ensuite le papier calque de façon que les côtés [OA] et [OB] soient superposables.
Déplie le papier calque. Sur le pli obtenu, place un point C puis trace la demi droite [OC].
À l’aide du rapporteur, vérifie que les angles AÔC et CÔB ont la même mesure.
On constate alors que AÔC = CÔB = 30°, c’est à dire que chaque angle mesure la moitié de l’angle AÔB.
La demi droite [OC] partage donc l’angle AÔB en deux angles de même mesure.
On appelle cette demi droite la bissectrice de l’angle AÔB.
Refais le même travail avec un angle AÔB de mesure 106° et observe le résultat.
La bissectrice d’un angle
Définition
La bissectrice d’un angle est la demi droite qui passe par le sommet de cet angle et qui le partage en deux angles de même mesure.
Si l’on considère un angle AÔB et sa bissectrice [OC], alors les deux angles obtenus sont égaux.
AÔC = CÔB = AÔB ÷ 2
La demi droite [OC] est donc appelée la bissectrice de l’angle AÔB.
Cette propriété est valable pour tous les angles, qu’ils soient aigus, droits ou obtus.
Angles de même mesure
Deux angles sont dits de même mesure lorsqu’ils ont la même ouverture, c’est à dire lorsqu’ils mesurent le même nombre de degrés.
Lorsque l’on trace la bissectrice d’un angle, celle ci partage l’angle en deux angles de même mesure.
Par exemple, si un angle mesure 80°, alors sa bissectrice le partage en deux angles qui mesurent chacun 40°.
Les angles AÔC et CÔB sont donc des angles de même mesure.
La notion d’angles de même mesure est importante en géométrie car elle permet de comparer des angles et de vérifier des constructions, notamment lors du tracé de la bissectrice.
Comment construire la bissectrice d’un angle
Construction de la bissectrice avec le compas et la règle
Pour construire la bissectrice d’un angle, on utilise une règle et un compas.
Soit un angle AÔB.
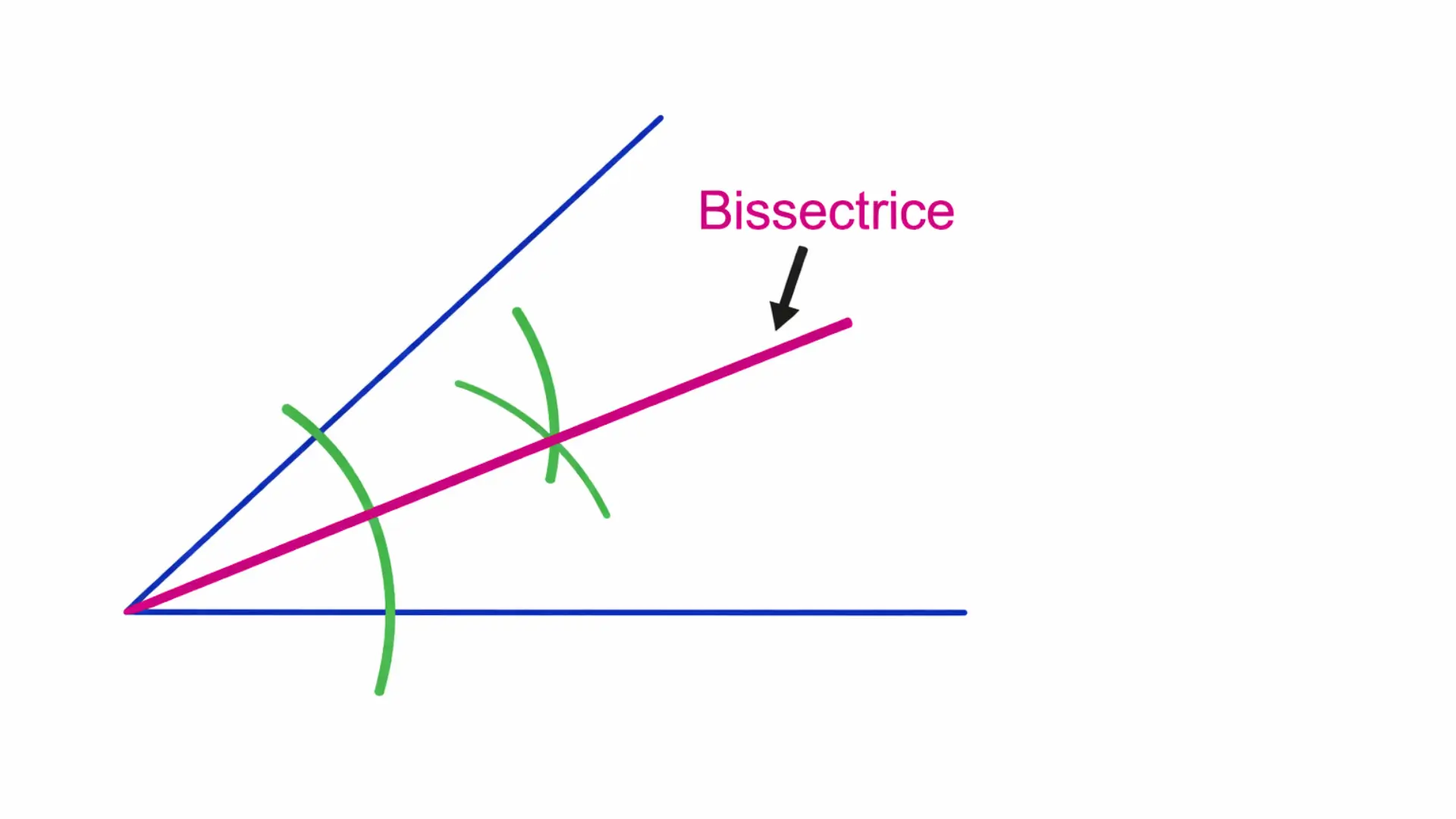
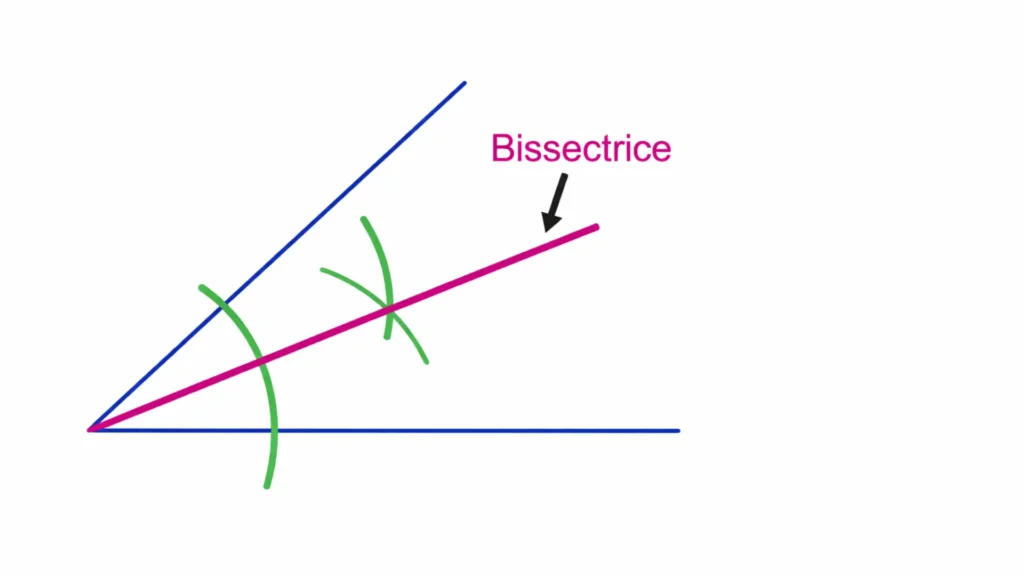
On place la pointe du compas sur le sommet O et on trace un arc de cercle qui coupe les côtés [OA] et [OB] en deux points que l’on appelle M et N.
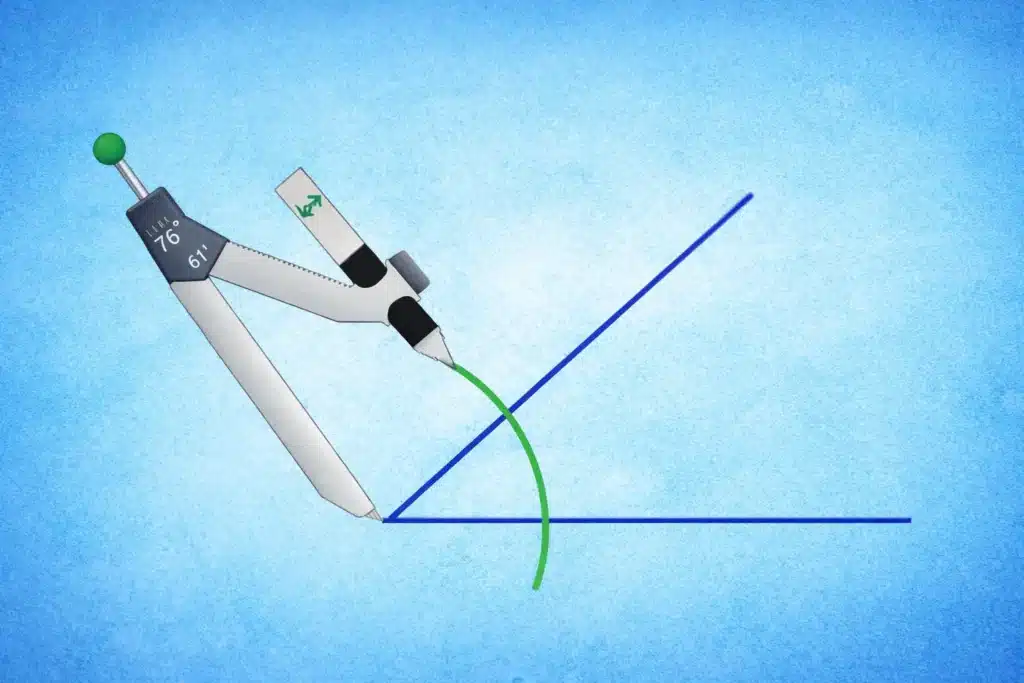
Sans changer l’ouverture du compas, on place la pointe du compas sur le point M et on trace un arc de cercle à l’intérieur de l’angle.
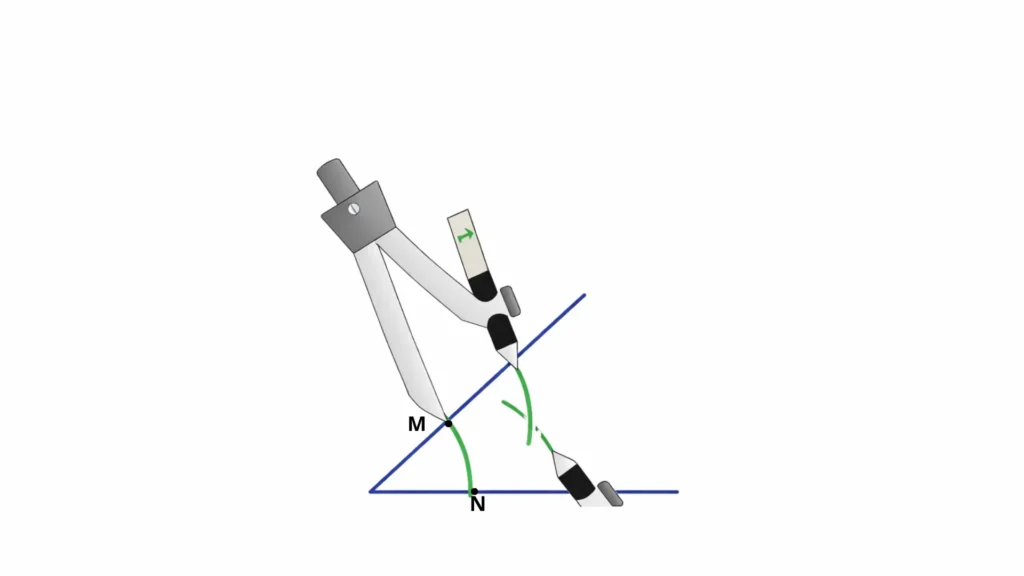
Avec la même ouverture du compas, on place ensuite la pointe sur le point N et on trace un autre arc de cercle qui coupe le précédent en un point P.
On trace alors la demi droite [OP).
La demi droite [OP) est la bissectrice de l’angle AÔB car elle partage cet angle en deux angles de même mesure.
Les angles complémentaires
Deux angles sont dits complémentaires lorsque la somme de leurs mesures est égale à 90°.
Autrement dit, si l’on additionne la mesure de deux angles complémentaires, on obtient un angle droit.
Par exemple, un angle de 30° et un angle de 60° sont des angles complémentaires car 30° + 60° = 90°.
Lorsque l’on trace la bissectrice d’un angle droit, celle ci partage l’angle droit en deux angles de même mesure. Chaque angle mesure alors 45°.
Les angles complémentaires sont souvent utilisés en géométrie pour vérifier des constructions et résoudre des exercices.
Les angles supplémentaires
Deux angles sont dits supplémentaires lorsque la somme de leurs mesures est égale à 180°.
Autrement dit, si l’on additionne la mesure de deux angles supplémentaires, on obtient un angle plat.
Par exemple, un angle de 70° et un angle de 110° sont des angles supplémentaires car 70° + 110° = 180°.
Lorsque l’on trace la bissectrice d’un angle plat, celle ci partage l’angle en deux angles de même mesure. Chaque angle mesure alors 90°.
Les angles supplémentaires permettent de comprendre la notion d’alignement et sont très utilisés dans les exercices de géométrie.
Exercices d’application : la bissectrice d’un angle
Exercice 1 : tracer la bissectrice avec le rapporteur
On considère un angle AÔB de mesure 74°.
- Trace l’angle AÔB.
- À l’aide du rapporteur, trace la demi-droite [OC] qui partage l’angle AÔB en deux angles de même mesure.
- Vérifie les mesures des angles AÔC et CÔB.
Complète :
AÔC = CÔB = ………°
Exercice 2 : tracer la bissectrice avec le compas et la règle
On considère un angle xÔy.
- Place la pointe du compas sur le sommet O et trace un arc de cercle qui coupe les côtés [Ox] et [Oy] en deux points A et B.
- Sans changer l’ouverture du compas, trace deux arcs de cercle de centres A et B qui se coupent en un point P.
- Trace la demi-droite [OP].
Indique pourquoi la demi-droite [OP] est la bissectrice de l’angle x Ô y.
Exercice 3 : angles complémentaires
Complète le tableau suivant sachant que les angles â et b̂ sont complémentaires.
| â | 18° | 27° | 41° | 56° |
|---|---|---|---|---|
| b̂ | … | … | … | … |
Rappel : deux angles complémentaires ont une somme égale à 90°.
Exercice 4 : angles supplémentaires
Complète le tableau suivant sachant que les angles ĉ et d̂ sont supplémentaires.
| ĉ | 65° | 98° | 124° | 157° |
|---|---|---|---|---|
| d̂ | … | … | … | … |
Rappel : deux angles supplémentaires ont une somme égale à 180°.
Exercice 5 : utiliser la bissectrice
On considère une demi-droite [OA].
Trace une demi-droite [OB] telle que BÔA = 68°.
- Trace la bissectrice [OC] de l’angle BÔA.
- Calcule la mesure des angles BÔC et CÔA.
Complète :
BÔC = CÔA = ………°.
Exercice 6 : raisonner sans mesurer
Les points A, O et C sont alignés.
Les points B, O et D sont alignés.
On sait que l’angle AÔB mesure 140°.
- Calcule la mesure de l’angle BÔC.
- Indique si les angles AÔB et BÔC sont complémentaires, supplémentaires ou de même mesure.
Justifie ta réponse.
Exercice 7 : triangle et bissectrice
ABC est un triangle rectangle en A.
On sait que l’angle ABC mesure 28°.
- Calcule la mesure de l’angle ACB.
- Trace la bissectrice de l’angle ABC.
- Calcule la mesure de chacun des angles formés par cette bissectrice.
Erreurs fréquentes à éviter
Lors de l’étude de la bissectrice d’un angle, certaines erreurs reviennent souvent chez les élèves. Il est important de les connaître afin de mieux les éviter.
Une erreur fréquente consiste à tracer une droite à l’intérieur de l’angle sans respecter les étapes de construction. Une droite tracée au hasard n’est pas une bissectrice. Pour qu’une demi droite soit la bissectrice d’un angle, elle doit obligatoirement partager l’angle en deux angles de même mesure.
Certains élèves oublient que la bissectrice passe toujours par le sommet de l’angle. Si la demi droite ne passe pas par le sommet, elle ne peut pas être la bissectrice.
Une autre erreur consiste à penser que la bissectrice dépend de la taille des côtés de l’angle. Or, seule la mesure de l’angle compte, et non la longueur des demi droites qui le forment.
Il arrive aussi que les élèves confondent les angles complémentaires et les angles supplémentaires. Les angles complémentaires ont une somme égale à 90°, tandis que les angles supplémentaires ont une somme égale à 180°.
Enfin, certains élèves pensent que deux angles complémentaires ou supplémentaires doivent être égaux. Ce n’est pas vrai. Ils doivent seulement avoir une somme donnée.
Conseils aux parents et aux enseignants
Pour bien comprendre la bissectrice d’un angle, il est important de privilégier la manipulation avant les calculs. L’utilisation du papier calque, du compas et de la règle aide l’élève à visualiser concrètement le partage d’un angle en deux angles de même mesure.
À la maison, les parents peuvent encourager l’enfant à expliquer à voix haute les étapes de construction. Dire ce que l’on fait permet de mieux mémoriser la méthode et de repérer plus facilement les erreurs.
Il est conseillé de vérifier que l’élève place correctement le sommet de l’angle avant de mesurer ou de tracer. Une petite erreur de positionnement peut fausser toute la construction.
Pour les enseignants, il est utile de proposer plusieurs types d’angles à travailler, aigus, droits et obtus, afin que l’élève comprenne que la bissectrice s’applique à tous les cas.
Enfin, il est important de rappeler régulièrement les notions d’angles complémentaires et supplémentaires, car elles sont souvent confondues. Revenir sur ces notions dans différents exercices renforce la compréhension et la réussite des élèves.
Mot du prof
La bissectrice d’un angle est une notion fondamentale en géométrie. Elle ne doit pas être apprise comme une simple définition, mais comprise à travers l’observation et la construction.
Prends toujours le temps de respecter les étapes de tracé, surtout lors de l’utilisation du compas. Une construction soignée est plus importante qu’un résultat rapide.
Si tu as un doute, vérifie toujours que les deux angles obtenus ont la même mesure. Cette vérification permet de confirmer que la bissectrice est correcte.
N’hésite pas à refaire plusieurs fois les constructions avec des angles différents. La géométrie s’apprend en pratiquant régulièrement.
Enfin, rappelle toi que comprendre la bissectrice aujourd’hui t’aidera plus tard pour d’autres notions importantes, comme les triangles, les droites remarquables et les figures géométriques plus complexes.
Télécharger le PDF
Pour t’aider à réviser efficacement la bissectrice d’un angle, un PDF est disponible en téléchargement. Il contient le cours résumé, les exercices d’application, les corrections détaillées ainsi qu’une page « À retenir » et les erreurs fréquentes à éviter.
Ce document peut être utilisé en classe, à la maison ou pour la révision avant une évaluation. Il est adapté aux élèves de CM2 et de 6e.
Clique sur le bouton ci dessous pour télécharger le PDF et t’entraîner pas à pas.
Conclusion
Dans cette leçon, nous avons découvert la bissectrice d’un angle à travers une activité de recherche, une définition claire et des exercices d’application. La bissectrice permet de partager un angle en deux angles de même mesure et s’utilise dans de nombreuses constructions géométriques.
La maîtrise de cette notion aide également à mieux comprendre les angles complémentaires et les angles supplémentaires, très présents dans les exercices de géométrie au CM2 et en 6e.
Pour progresser, il est important de s’entraîner régulièrement, de refaire les constructions avec soin et de vérifier les mesures à chaque étape. Les exercices corrigés et le PDF à télécharger permettent de consolider les acquis à la maison ou en classe.
Retrouve cette leçon ainsi que d’autres cours et fiches de mathématiques clairs et progressifs sur Pinterest, afin de réviser efficacement et d’apprendre pas à pas.
FAQ : Questions fréquentes sur la bissectrice d’un angle
Qu’est ce que la bissectrice d’un angle ?
La bissectrice d’un angle est la demi droite qui partage cet angle en deux angles de même mesure. Elle passe toujours par le sommet de l’angle.
La bissectrice partage -t-elle toujours un angle en deux angles égaux ?
Oui. Par définition, la bissectrice partage toujours un angle en deux angles exactement égaux, quelle que soit la mesure de l’angle.
Peut on construire une bissectrice sans compas ?
Il est possible d’utiliser un rapporteur pour placer la moitié de la mesure de l’angle, mais la méthode officielle en géométrie utilise le compas et la règle.
La bissectrice dépend-elle de la longueur des côtés d’un angle ?
Non. La bissectrice dépend uniquement de la mesure de l’angle et non de la longueur des demi droites qui le forment.
Quelle est la différence entre angles complémentaires et angles supplémentaires ?
Deux angles sont complémentaires lorsque la somme de leurs mesures est égale à 90°. Deux angles sont supplémentaires lorsque la somme de leurs mesures est égale à 180°.
Cette leçon est elle au programme du CM2 et de la 6e ?
Oui. La bissectrice d’un angle fait partie du programme de géométrie au CM2 et en 6e.