Le volume du cube et du parallélépipède est une notion fondamentale en géométrie qui permet de mesurer l’espace occupé par certains solides. Dans la vie quotidienne, de nombreux objets ont la forme d’un cube ou d’un parallélépipède rectangle, comme les boîtes, les cartons ou les briques.
Calculer un volume permet de savoir quelle quantité d’espace un solide occupe. Pour cela, on utilise des unités de volume et des formules adaptées à chaque type de solide.
Dans cet article, nous allons apprendre à comprendre la notion de volume, à calculer le volume du cube et celui du parallélépipède rectangle, puis à appliquer ces connaissances à travers des exemples et des exercices.
À la fin de cette leçon, l’élève sera capable d’utiliser correctement les formules et de calculer un volume sans se tromper.
Table of Contents
Qu’est-ce que le volume d’un solide ?
Le volume d’un solide représente l’espace qu’il occupe. Il permet de savoir quelle place prend un objet dans l’espace, quelle que soit sa forme.
Par exemple, une boîte, un cube ou un carton n’occupent pas la même quantité d’espace. Leur volume peut être plus grand ou plus petit selon leurs dimensions.
Le volume se mesure à l’aide d’unités de volume, qui sont des unités cubiques. Les unités les plus utilisées sont :
- le centimètre cube (cm³)
- le décimètre cube (dm³)
- le mètre cube (m³)
Le volume ne doit pas être confondu avec l’aire.
- L’aire mesure une surface.
- Le volume mesure un espace en trois dimensions.
Pour calculer le volume d’un solide, on utilise une formule qui dépend de sa forme. Dans cette leçon, nous allons étudier deux solides particuliers : le cube et le parallélépipède rectangle.
Comprendre le volume à l’aide de cubes (unité U)
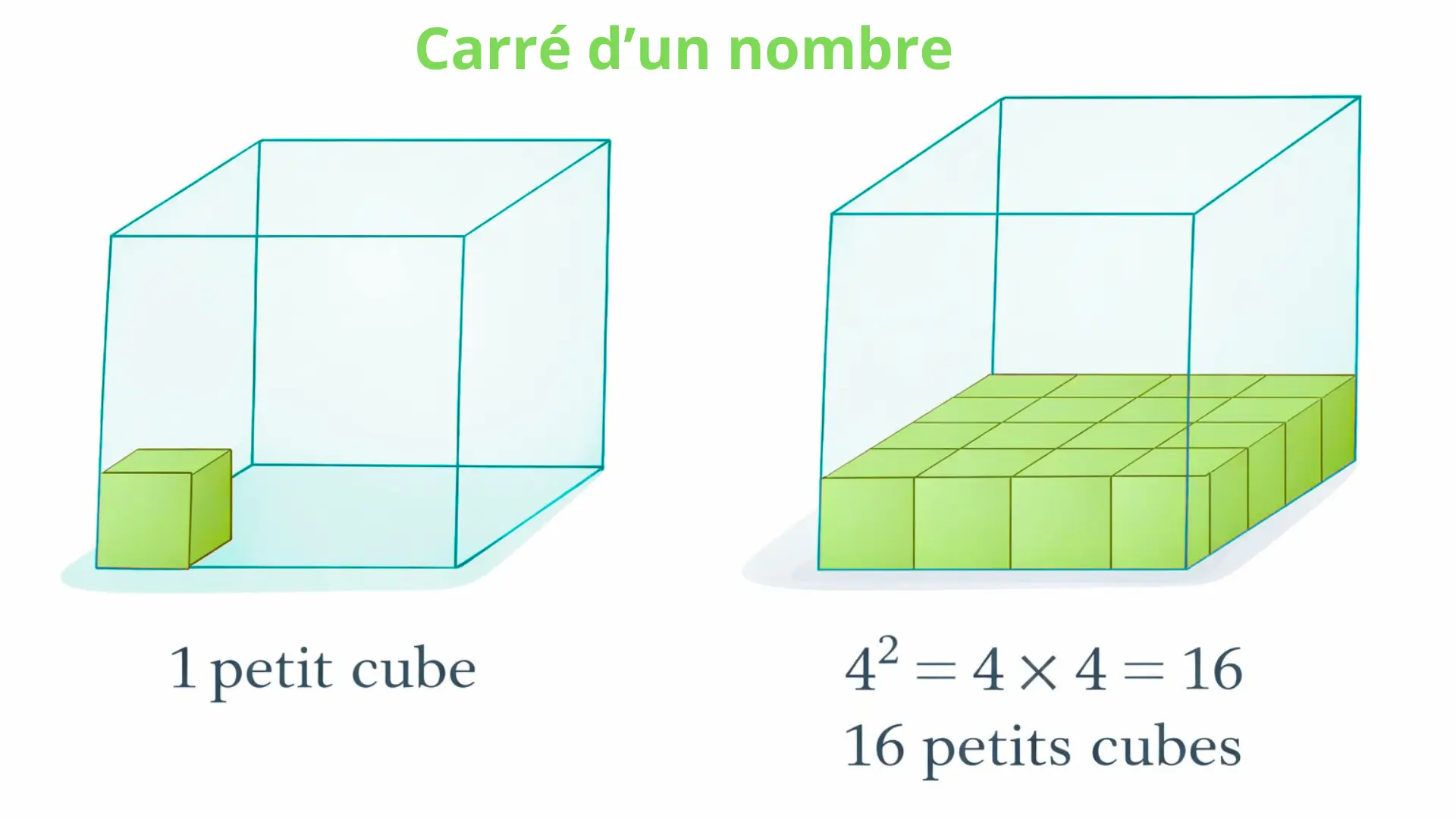
Pour comprendre ce qu’est le volume d’un solide, on commence par utiliser des unités arbitraires, comme des petits cubes identiques.
On choisit le volume d’un petit cube comme unité de volume, notée U.
Le volume d’un cube à l’aide de l’unité U
On considère un grand cube construit avec plusieurs petits cubes identiques.
Chaque petit cube a un volume égal à 1 U.
Le volume du grand cube correspond alors au nombre total de petits cubes qui le composent.
Pour trouver le volume :
- on compte le nombre de cubes sur une arête
- on compte le nombre de cubes sur une autre arête
- on compte le nombre de cubes en hauteur
Le volume du grand cube est obtenu en multipliant ces trois nombres.
Exemple :
Si le grand cube contient :
- 2 cubes en longueur
- 2 cubes en largeur
- 2 cubes en hauteur
Alors son volume est :
V = 2 × 2 × 2 = 8 U
On vérifie ainsi que le volume dépend du nombre de cubes qui remplissent l’espace.

Le volume d’un parallélépipède rectangle à l’aide de l’unité U
On considère maintenant un parallélépipède rectangle formé avec des petits cubes identiques de volume U.
Pour déterminer son volume :
- on compte le nombre de cubes selon la longueur
- on compte le nombre de cubes selon la largeur
- on compte le nombre de cubes selon la hauteur
Le volume du parallélépipède rectangle est égal au produit de ces trois nombres.
Exemple :
Si le solide contient :
- 3 cubes en longueur
- 2 cubes en largeur
- 4 cubes en hauteur
Alors son volume est :
V = 3 × 2 × 4 = 24 U
Ce qu’il faut retenir
- Le volume mesure l’espace occupé par un solide
- Le volume correspond au nombre d’unités de volume U nécessaires pour remplir ce solide
- Pour un cube ou un parallélépipède rectangle, le volume se calcule par une multiplication de trois dimensions
Cette méthode permet de comprendre la formule du volume, avant d’utiliser des unités comme le cm³ ou le m³.
Déduire la formule du volume du cube
Dans la partie précédente, nous avons calculé le volume d’un cube en comptant le nombre de petits cubes identiques qui le composent.
On a vu que, pour un cube :
- le nombre de cubes est le même en longueur, en largeur et en hauteur
- ces trois dimensions sont donc égales
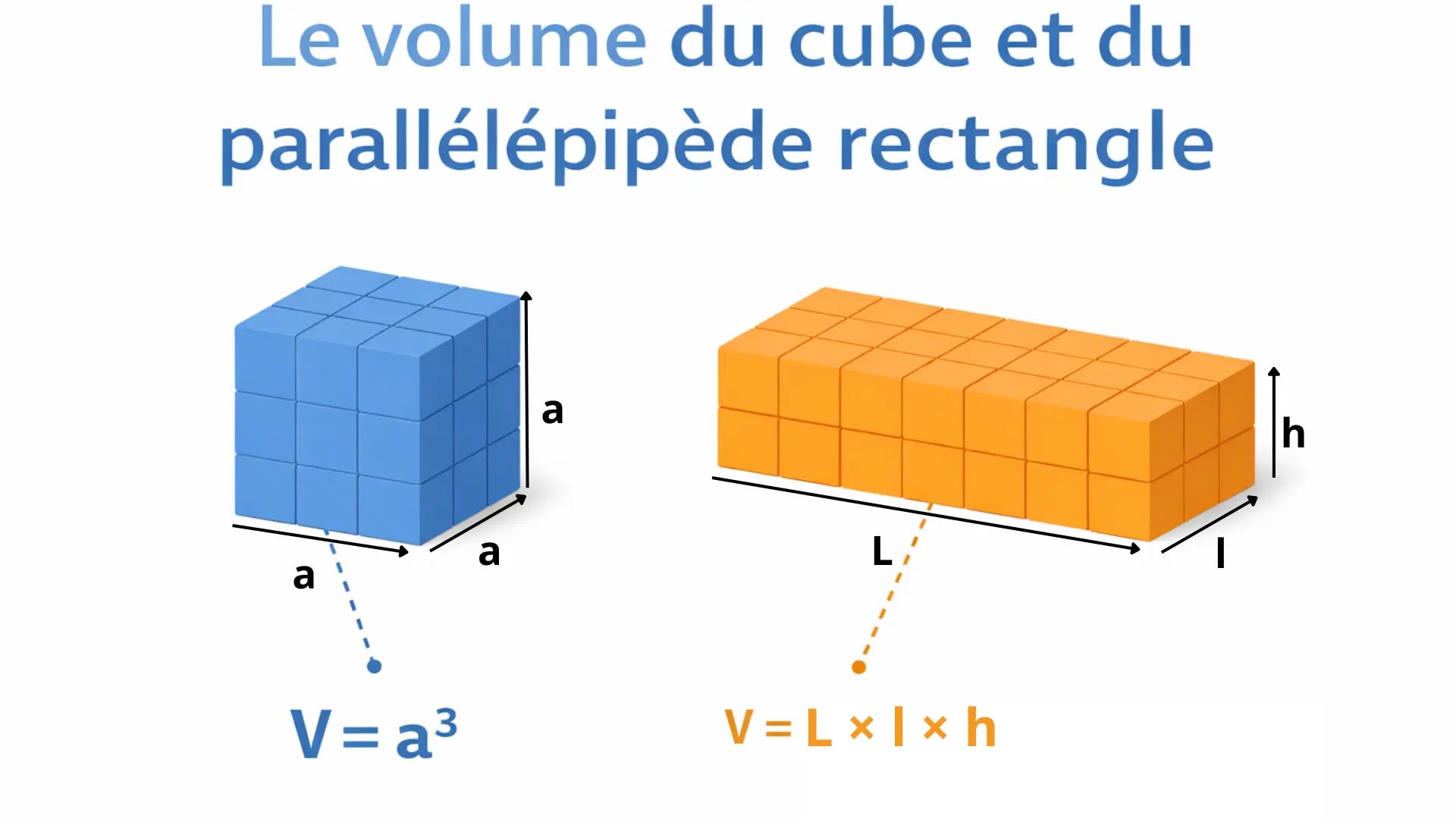
Formule du volume du cube
Si la longueur de l’arête du cube est notée a, alors :
- longueur = a
- largeur = a
- hauteur = a
Le volume du cube est obtenu en multipliant ces trois dimensions :
V = a × a × a
On peut aussi écrire cette formule sous la forme :
V = a³
Cette formule permet de calculer rapidement le volume d’un cube.
Exemple de calcul
Un cube a une arête de 4 cm.
On applique la formule :
V = 4 × 4 × 4
V = 64 cm³
Le volume du cube est donc 64 cm³.
Ce qu’il faut retenir
- Un cube a trois dimensions égales
- Son volume se calcule en multipliant la longueur de l’arête par elle-même trois fois
- Le résultat s’exprime toujours en unités cubiques (cm³, dm³, m³)
Déduire la formule du volume du parallélépipède rectangle
Un parallélépipède rectangle est un solide qui possède :
- une longueur
- une largeur
- une hauteur
Ces trois dimensions ne sont pas forcément égales, contrairement au cube.
Formule du volume du parallélépipède rectangle
Pour calculer le volume d’un parallélépipède rectangle, on multiplie :
- la longueur
- par la largeur
- par la hauteur
La formule est donc :
V = longueur × largeur × hauteur
Cette formule permet de calculer le volume de tout parallélépipède rectangle.
Exemple de calcul
Un parallélépipède rectangle a :
- une longueur de 5 cm
- une largeur de 3 cm
- une hauteur de 4 cm
On applique la formule :
V = 5 × 3 × 4
V = 60 cm³
Le volume du parallélépipède rectangle est donc 60 cm³.
Ce qu’il faut retenir
- Le parallélépipède rectangle possède trois dimensions différentes
- Son volume se calcule en multipliant la longueur, la largeur et la hauteur
- Le résultat s’exprime toujours en unités cubiques
Problèmes résolus pas à pas
Problème 1 : Volume d’un cube
Un cube a une arête de 6 cm.
Calculer le volume de ce cube.
Étape 1 : Identifier le solide
Il s’agit d’un cube.
Étape 2 : Écrire la formule adaptée
Pour un cube :
V = a³
Étape 3 : Remplacer par la valeur donnée
V = 6 × 6 × 6
Étape 4 : Effectuer le calcul
V = 216
Étape 5 : Écrire la réponse avec l’unité
Le volume du cube est 216 cm³.
Problème 2 : Volume d’un parallélépipède rectangle
Un parallélépipède rectangle a :
- une longueur de 8 cm
- une largeur de 5 cm
- une hauteur de 4 cm
Calculer son volume.
Étape 1 : Identifier le solide
Il s’agit d’un parallélépipède rectangle.
Étape 2 : Écrire la formule adaptée
V = longueur × largeur × hauteur
Étape 3 : Remplacer par les valeurs
V = 8 × 5 × 4
Étape 4 : Effectuer le calcul
V = 160
Étape 5 : Écrire la réponse avec l’unité
Le volume du parallélépipède rectangle est 160 cm³.
Problème 3 : Comparer deux volumes
Un cube a une arête de 4 cm.
Un parallélépipède rectangle a pour dimensions 4 cm, 4 cm et 4 cm.
Calculer le volume de chaque solide.
Pour le cube :
V = 4³ = 64 cm³
Pour le parallélépipède rectangle :
V = 4 × 4 × 4 = 64 cm³
Les deux solides ont donc le même volume.
Exercices d’application
Exercice 1 : Calculer le volume d’un cube
Calculer le volume de chaque cube.
- Un cube a une arête de 3 cm.
- Un cube a une arête de 5 cm.
- Un cube a une arête de 7 cm.
Exprimer les résultats en cm³.
Exercice 2 : Calculer le volume d’un parallélépipède rectangle
Calculer le volume de chaque parallélépipède rectangle.
- Longueur = 6 cm, largeur = 4 cm, hauteur = 3 cm
- Longueur = 8 cm, largeur = 5 cm, hauteur = 2 cm
- Longueur = 10 cm, largeur = 4 cm, hauteur = 6 cm
Exprimer les résultats en cm³.
Exercice 3 : Compléter
Compléter les phrases suivantes.
- Le volume d’un cube se calcule en multipliant ………… par ………… par …………
- La formule du volume du cube est : …………
- La formule du volume du parallélépipède rectangle est : …………
Exercice 4 : Comparer des volumes
- Un cube a une arête de 4 cm.
Un parallélépipède rectangle a pour dimensions 4 cm, 4 cm et 4 cm.
Calculer leurs volumes et comparer. - Un cube a une arête de 6 cm.
Un parallélépipède rectangle a pour dimensions 9 cm, 4 cm et 3 cm.
Calculer les volumes et dire lequel est le plus grand.
Exercice 5 : Problème
Un carton a la forme d’un parallélépipède rectangle de longueur 12 cm, de largeur 8 cm et de hauteur 5 cm.
- Calculer le volume du carton.
- Exprimer le résultat en cm³.
Erreurs fréquentes
Lors du calcul du volume du cube et du parallélépipède rectangle, certaines erreurs reviennent souvent. Les connaître permet de mieux les éviter.
1. Confondre aire et volume
L’aire mesure une surface, alors que le volume mesure un espace.
Utiliser une formule d’aire au lieu d’une formule de volume est une erreur fréquente.
2. Oublier une dimension dans le calcul
Pour calculer un volume, il faut toujours multiplier trois dimensions.
Oublier la hauteur ou l’une des dimensions donne un résultat faux.
3. Utiliser une mauvaise formule
Chaque solide a sa propre formule :
- cube : V = a³
- parallélépipède rectangle : V = longueur × largeur × hauteur
Confondre ces deux formules conduit à une erreur de calcul.
4. Oublier l’unité du volume
Un volume doit toujours être exprimé en unités cubiques, comme cm³ ou m³.
Une réponse sans unité est incomplète.
5. Ne pas vérifier la cohérence du résultat
Un volume doit être cohérent avec les dimensions du solide.
Un petit objet ne peut pas avoir un volume très grand.
Voici la section Conseils pour les profs et les parents, rédigée de façon simple, pratique et adaptée au niveau C6, comme dans un manuel scolaire.
Conseils pour les profs et les parents
L’apprentissage du volume du cube et du parallélépipède rectangle est plus efficace lorsqu’il est concret et progressif.
Conseils pour les profs
Il est recommandé de commencer par des manipulations avec des cubes ou des pavés afin d’aider les élèves à visualiser le volume. L’utilisation d’objets de la vie courante, comme des boîtes ou des cartons, permet de donner du sens aux formules.
Il est important de faire le lien entre le comptage des cubes et la formule de calcul du volume. Demander aux élèves d’expliquer leur démarche à l’oral aide à consolider la compréhension.
Varier les exercices en proposant des calculs simples puis des problèmes permet de répondre aux besoins de tous les élèves.
Conseils pour les parents
À la maison, il est utile de montrer des objets en forme de cube ou de parallélépipède rectangle, comme des boîtes ou des briques, et de demander à l’enfant d’identifier leurs dimensions.
Encourager l’enfant à écrire les formules avant de calculer et à vérifier l’unité du résultat l’aide à éviter les erreurs. L’essentiel est de comprendre la méthode plutôt que d’aller trop vite.
Mot du prof
Le calcul du volume du cube et du parallélépipède rectangle est une notion essentielle en géométrie. Elle permet de mieux comprendre l’espace et de résoudre des situations concrètes de la vie quotidienne.
Prends toujours le temps d’identifier le solide, d’écrire la formule correcte et de vérifier les unités. N’oublie pas que le volume mesure un espace et qu’il s’exprime toujours en unités cubiques.
Avec de l’entraînement et de la rigueur, le calcul des volumes deviendra de plus en plus simple. Chaque exercice est une occasion de progresser et de renforcer ta confiance en mathématiques.
Exercices sur le volume du cube et du parallélépipède (PDF)
Pour renforcer la compréhension et s’entraîner davantage, vous pouvez télécharger le PDF d’exercices . Ce document regroupe les formules essentielles, des exemples expliqués et une série d’exercices progressifs sur le volume du cube et du parallélépipède rectangle. Il est idéal pour réviser à la maison, s’entraîner en classe ou consolider les acquis avant une évaluation.
Conclusion
Dans cette leçon, nous avons appris à comprendre le volume à l’aide d’unités simples, puis à calculer le volume du cube et du parallélépipède rectangle à l’aide de formules adaptées. Nous avons vu comment ces formules sont liées au comptage de cubes et pourquoi le volume s’exprime toujours en unités cubiques.
Grâce aux exemples et aux exercices proposés, l’élève est désormais capable de reconnaître ces solides, de choisir la bonne formule et de calculer leur volume correctement, tout en vérifiant la cohérence des résultats.
Pour s’entraîner davantage et revoir les notions essentielles, des exercices et des rappels de cours sont également partagés sur Pinterest. Ils peuvent être enregistrés, consultés plus tard ou partagés avec des camarades pour réviser ensemble.
La maîtrise du calcul des volumes constitue une base importante pour la suite des apprentissages en géométrie et pour résoudre des situations concrètes de la vie quotidienne.
FAQ : Le volume du cube et du parallélépipède
Quelle est la différence entre le volume et l’aire ?
L’aire mesure une surface, tandis que le volume mesure l’espace occupé par un solide. Le volume se calcule toujours avec trois dimensions et s’exprime en unités cubiques.
Pourquoi les unités du volume sont-elles cubiques ?
Parce que le volume mesure un espace en trois dimensions. On utilise donc des unités comme cm³, dm³ ou m³.
Quelle formule utiliser pour calculer le volume d’un cube ?
Pour un cube, toutes les arêtes sont égales.
La formule est : V = a³, où a représente la longueur de l’arête.
Quelle formule utiliser pour calculer le volume d’un parallélépipède rectangle ?
On multiplie la longueur, la largeur et la hauteur.
La formule est : V = longueur × largeur × hauteur.
Peut-on comparer le volume d’un cube et celui d’un parallélépipède rectangle ?
Oui, à condition que les volumes soient exprimés dans la même unité. Deux solides de formes différentes peuvent avoir le même volume.
Faut-il toujours écrire l’unité dans la réponse ?
Oui. Une réponse sans unité est incomplète. Le volume doit toujours être exprimé en unités cubiques.