Les multiples et les diviseurs CM2 sont des notions essentielles pour progresser en calcul et en résolution de problèmes. Comprendre ces deux idées aide à mieux diviser, regrouper ou partager des objets équitablement. Dans cette leçon, tu apprendras à reconnaître les multiples et les diviseurs, à les utiliser dans différents calculs et à appliquer les critères de divisibilité pour aller plus vite. Tu pourras aussi télécharger une fiche complète avec le cours, les exercices et leurs corrigés.
Introduction
Tu t’es déjà demandé comment partager équitablement des bonbons entre tes amis ou comment regrouper des objets par paquets égaux ? Les multiples et les diviseurs sont deux notions qui t’aident à comprendre tout cela facilement. Ce sont des outils importants en mathématiques pour apprendre à compter, diviser et résoudre des problèmes du quotidien.
Dans cette leçon de mathématiques CM2, tu vas découvrir ce que sont les multiples et les diviseurs, comment les reconnaître et comment les utiliser dans différents calculs. Tu verras aussi des astuces simples, des exercices corrigés et une fiche PDF à télécharger pour t’entraîner à la maison.
Table of Contents
Table of Contents
Objectifs de la leçon :
- Comprendre la différence entre un multiple et un diviseur.
- Savoir calculer les multiples d’un nombre.
- Trouver les diviseurs d’un nombre.
- Utiliser les critères de divisibilité pour aller plus vite.
Les multiples : des nombres qui grandissent ensemble
Un multiple est le résultat d’une multiplication. Par exemple, les multiples de 3 sont les résultats des multiplications suivantes :
3 × 0 = 0 3 × 1 = 3 3 × 2 = 6 3 × 3 = 9 3 × 4 = 12
On dit donc que 0, 3, 6, 9, 12… sont des multiples de 3.
Un multiple est donc un nombre qui “grandit” régulièrement en suivant une règle de multiplication.
Comment trouver les multiples d’un nombre ?
Pour trouver les multiples d’un nombre, il suffit de le multiplier par 0, 1, 2, 3, 4, etc.
Chaque résultat obtenu est un multiple.
Exemple :
Les multiples de 5 sont :
5 × 0 = 0 5 × 1 = 5 5 × 2 = 10 5 × 3 = 15 5 × 4 = 20
Les multiples de 5 sont donc 0, 5, 10, 15, 20, 25, 30…
Les propriétés des multiples :
- Un nombre a une infinité de multiples.
- 0 est un multiple de tous les nombres.
- Chaque nombre est un multiple de lui-même.
Petit défi :
- Trouve les 5 premiers multiples de 4.
- Est-ce que 24 est un multiple de 6 ? Explique ta réponse.
- Donne un multiple de 8 compris entre 30 et 50.
Les diviseurs : les nombres qui partagent juste
Un diviseur est un nombre qui partage un autre nombre sans reste. Autrement dit, quand on divise un nombre par son diviseur, le reste est égal à zéro.
Exemple :
12 ÷ 3 = 4 → il n’y a pas de reste.
On dit donc que 3 est un diviseur de 12.
Et comme 12 = 3 × 4, on voit que 12 est un multiple de 3, et 3 est un diviseur de 12.
Comment trouver les diviseurs d’un nombre ?
Pour trouver tous les diviseurs d’un nombre, on cherche toutes les multiplications qui permettent d’obtenir ce nombre.
Exemple avec 12 :
1 × 12 = 12 2 × 6 = 12 3 × 4 = 12
Les diviseurs de 12 sont donc 1, 2, 3, 4, 6 et 12.
Astuce : pense en “paires de diviseurs”. Si 2 divise 12, alors 12 ÷ 2 = 6, donc 6 est aussi un diviseur.
Les propriétés des diviseurs :
- Un nombre a un nombre limité de diviseurs.
- 1 est un diviseur de tous les nombres.
- Chaque nombre est diviseur de lui-même.
- Si un nombre A est diviseur de B, alors B est multiple de A.
Petit défi :
- Trouve tous les diviseurs de 18.
- Le nombre 7 est-il un diviseur de 35 ? Et de 30 ?
- Combien de diviseurs possède le nombre 24 ?
Le lien entre les multiples et les diviseurs
Les multiples et les diviseurs sont liés entre eux par la multiplication et la division.
La relation “si… alors…” :
- Si un nombre A est un multiple d’un nombre B, alors B est un diviseur de A.
- Et inversement : si B est un diviseur de A, alors A est un multiple de B.
Exemples :
20 est un multiple de 5 → donc 5 est un diviseur de 20.
12 est un multiple de 3 → donc 3 est un diviseur de 12.
Comment les relier facilement ?
Petit nombre × autre petit nombre = grand nombre
3 × 4 = 12 → 12 est un multiple de 3 et de 4, et 3 et 4 sont des diviseurs de 12.
Petit défi :
- Complète la phrase : Si 30 est un multiple de 5, alors…
- Trouve un nombre qui est à la fois multiple de 4 et multiple de 6.
- Peux-tu citer un nombre qui est diviseur de 18 et diviseur de 24 ?
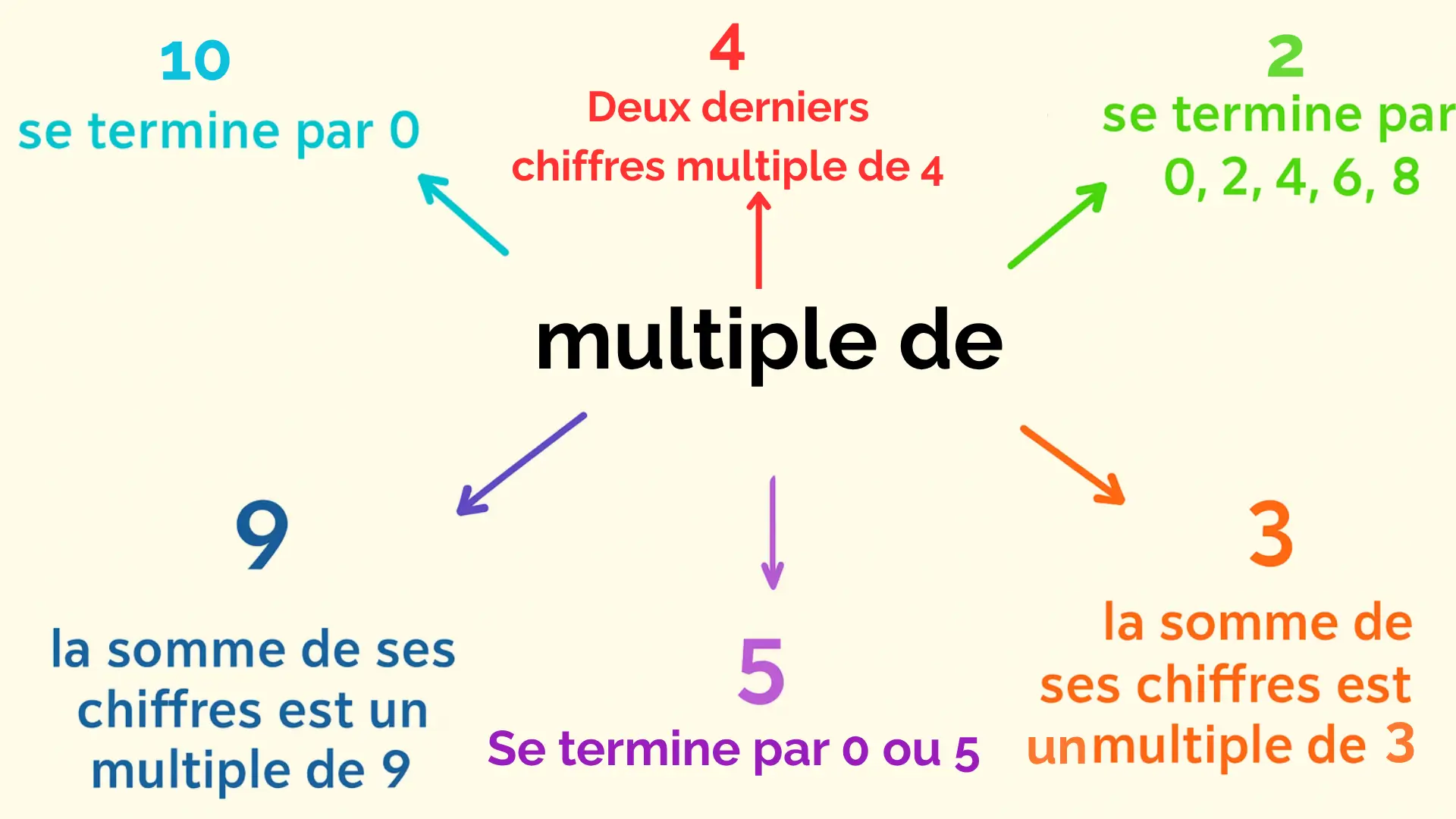
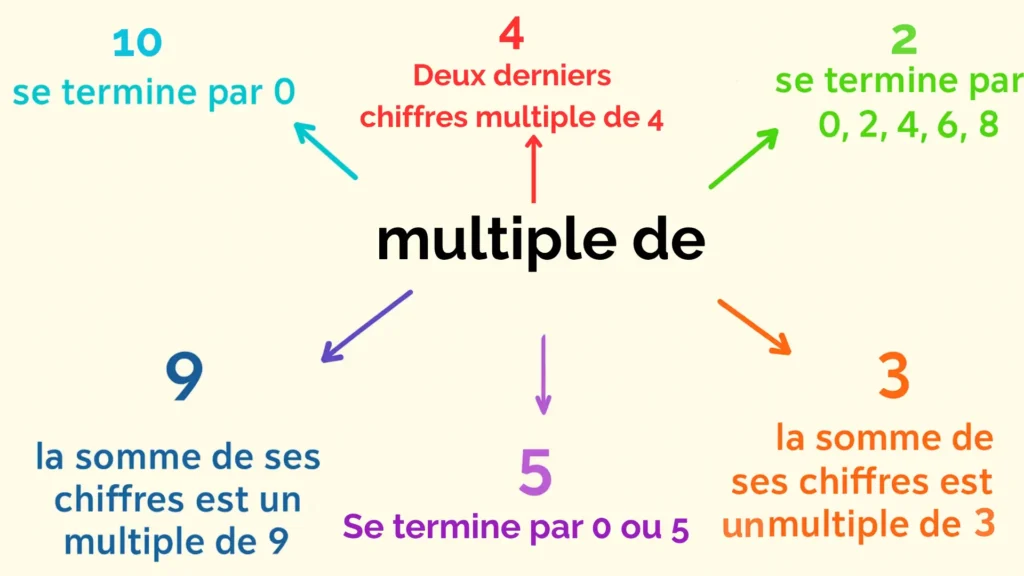
Les critères de divisibilité
Les critères de divisibilité sont des règles simples qui permettent de savoir si un nombre est divisible par un autre sans faire la division.
Divisible par 2 :
Un nombre est divisible par 2 s’il est pair, c’est-à-dire s’il se termine par 0, 2, 4, 6 ou 8.
Exemples : 18, 42 et 60 sont divisibles par 2.
Divisible par 3 :
Un nombre est divisible par 3 si la somme de ses chiffres est un multiple de 3.
Exemple : 123 → 1 + 2 + 3 = 6, et 6 est un multiple de 3, donc 123 est divisible par 3.
Divisible par 4 :
Un nombre est divisible par 4 si les deux derniers chiffres forment un multiple de 4.
Exemples : 312 (les deux derniers chiffres 12 → multiple de 4), 318 non.
Divisible par 5 :
Un nombre est divisible par 5 s’il se termine par 0 ou 5.
Exemples : 45, 60 et 85 sont divisibles par 5.
Divisible par 9 :
Un nombre est divisible par 9 si la somme de ses chiffres est un multiple de 9.
Exemple : 234 → 2 + 3 + 4 = 9 → divisible par 9.
Divisible par 10 :
Un nombre est divisible par 10 s’il se termine par 0.
Exemple : 80, 140 et 1230 sont divisibles par 10.
Récapitulatif :
| Nombre | Règle de divisibilité | Exemples |
|---|---|---|
| 2 | Se termine par 0, 2, 4, 6 ou 8 | 18, 42 |
| 3 | Somme des chiffres multiple de 3 | 123 |
| 4 | Deux derniers chiffres multiple de 4 | 312 |
| 5 | Se termine par 0 ou 5 | 45, 60 |
| 9 | Somme des chiffres multiple de 9 | 234 |
| 10 | Se termine par 0 | 80, 140 |
Exercices rapides :
- Sans diviser, dis si les nombres suivants sont divisibles par 2, 3, 5, 9 ou 10 : 126, 245, 360, 432
- Trouve un nombre divisible à la fois par 2 et 5.
- Trouve un nombre divisible par 3 mais pas par 9.
Les erreurs fréquentes à éviter
Erreur n°1 : Confondre “multiple” et “diviseur”
Les multiples sont les résultats des multiplications, donc ils grandissent. Les diviseurs sont ceux qui partagent sans reste, donc ils sont plus petits.
Erreur n°2 : Oublier le 0 pour les multiples et le 1 pour les diviseurs
0 est un multiple de tous les nombres. 1 est un diviseur de tous les nombres.
Erreur n°3 : Penser qu’il existe un nombre limité de multiples
Les multiples continuent à l’infini.
Erreur n°4 : Oublier un diviseur
Tout nombre est diviseur de lui-même.
Erreur n°5 : Mal comprendre “divisible par” et “multiple de”
Dire qu’un nombre est divisible par un autre signifie qu’il est un multiple de cet autre.
Exercices et corrigés
Exercice 1 : Trouve les 5 premiers multiples de :
3 → 0, 3, 6, 9, 12
4 → 0, 4, 8, 12, 16
6 → 0, 6, 12, 18, 24
9 → 0, 9, 18, 27, 36
Exercice 2 : Trouve tous les diviseurs de :

12 → 1, 2, 3, 4, 6, 12
18 → 1, 2, 3, 6, 9, 18
24 → 1, 2, 3, 4, 6, 8, 12, 24
36 → 1, 2, 3, 4, 6, 9, 12, 18, 36
Exercice 3 : Vrai ou faux
20 est un multiple de 5 → vrai
7 est un diviseur de 30 → faux
0 est un multiple de tous les nombres → vrai
1 est un diviseur de tous les nombres → vrai
Exercice 4 : Problème
Dans une classe, il y a 24 élèves.
L’enseignant souhaite les répartir en groupes égaux, sans qu’il reste d’élèves seuls.
Question :
Quelles sont toutes les répartitions possibles ?
Correction :
Pour trouver les différentes répartitions, il faut chercher les diviseurs de 24.
Les diviseurs de 24 sont : 1, 2, 3, 4, 6, 8, 12 et 24.
On peut donc former :
- 1 groupe de 24 élèves
- 2 groupes de 12 élèves
- 3 groupes de 8 élèves
- 4 groupes de 6 élèves
- 6 groupes de 4 élèves
- 8 groupes de 3 élèves
- 12 groupes de 2 élèves
- 24 groupes d’un élève
Télécharge ta fiche de révision – Multiples et diviseurs CM2
Tu veux t’exercer tranquillement à la maison ?
Télécharge la fiche complète de révision sur les multiples et les diviseurs CM2.
Elle contient le cours bien expliqué, des exemples clairs, des exercices variés avec leur corrigé et un design prêt à imprimer pour t’aider à t’entraîner seul(e) ou avec ton enseignant(e).
C’est idéal pour préparer une évaluation ou réviser avant un contrôle.
Télécharger la fiche PDF : Multiples et diviseurs CM2
Conclusion
Les multiples et les diviseurs sont essentiels pour bien comprendre les nombres. Ils aident à mieux diviser, partager et repérer les régularités dans les suites de nombres. Grâce aux critères de divisibilité, il est possible de vérifier rapidement si un nombre est divisible sans faire de calcul compliqué. Continue à t’exercer régulièrement : plus tu pratiques, plus ces notions deviendront simples et naturelles.
Retrouve aussi d’autres fiches et idées d’activités sur Pinterest .
Le mot du prof
Bravo pour ton travail. Si tu es arrivé jusqu’ici, c’est que tu as bien compris la différence entre multiple et diviseur. Ces notions te serviront beaucoup pour apprendre les nombres premiers et la simplification des fractions. Continue à t’exercer un peu chaque jour, imprime ta fiche et amuse -toi à repérer des multiples et des diviseurs autour de toi : dans les prix, les horaires, les jeux ou les objets du quotidien. Les mathématiques sont partout, il suffit d’ouvrir les yeux.
Si tu trouves certaines parties difficiles à comprendre ou si tu veux que j’explique une autre leçon, écris- moi directement via le site ou sur Pinterest
FAQ : tes questions sur les multiples et les diviseurs
Est-ce qu’un nombre peut être à la fois un multiple et un diviseur ?
Oui. Par exemple, 6 est un multiple de 3 et un diviseur de 12.
Est-ce que tous les nombres ont le même nombre de multiples ?
Non. Tous les nombres ont une infinité de multiples, mais pas le même nombre de diviseurs.
Pourquoi 0 est-il un multiple de tous les nombres ?
Parce que tout nombre multiplié par 0 donne 0.
Est-ce que 1 est un multiple de tous les nombres ?
Non, 1 est un diviseur de tous les nombres, mais pas un multiple.
Y a-t-il une méthode pour trouver tous les diviseurs d’un nombre sans en oublier ?
Oui. Cherche toutes les paires de nombres dont le produit donne le nombre voulu.
À quoi servent les multiples et les diviseurs dans la vie de tous les jours ?
Les multiples servent à regrouper ou mesurer, les diviseurs servent à partager équitablement.