La proportionnalité : intérêt intervient très souvent dans les situations de la vie quotidienne, en particulier lorsqu’on parle d’argent, de pourcentages et d’intérêts bancaires. Lorsqu’une personne place une somme d’argent dans une banque, cette somme peut augmenter au bout d’un certain temps grâce à un intérêt.
Cet intérêt dépend directement du capital placé et du taux appliqué. Il existe donc une relation de proportionnalité entre le capital, le taux et l’intérêt. Comprendre cette relation permet de calculer correctement les gains obtenus après une année ou plus.
Dans cette leçon, nous allons apprendre à utiliser la proportionnalité pour calculer l’intérêt annuel, le capital ou le taux, à l’aide de formules simples et d’exemples concrets.
Table of Contents
Comprendre les notions de base
Avant d’effectuer des calculs, il est important de bien comprendre les notions utilisées dans la proportionnalité appliquée aux placements d’argent.
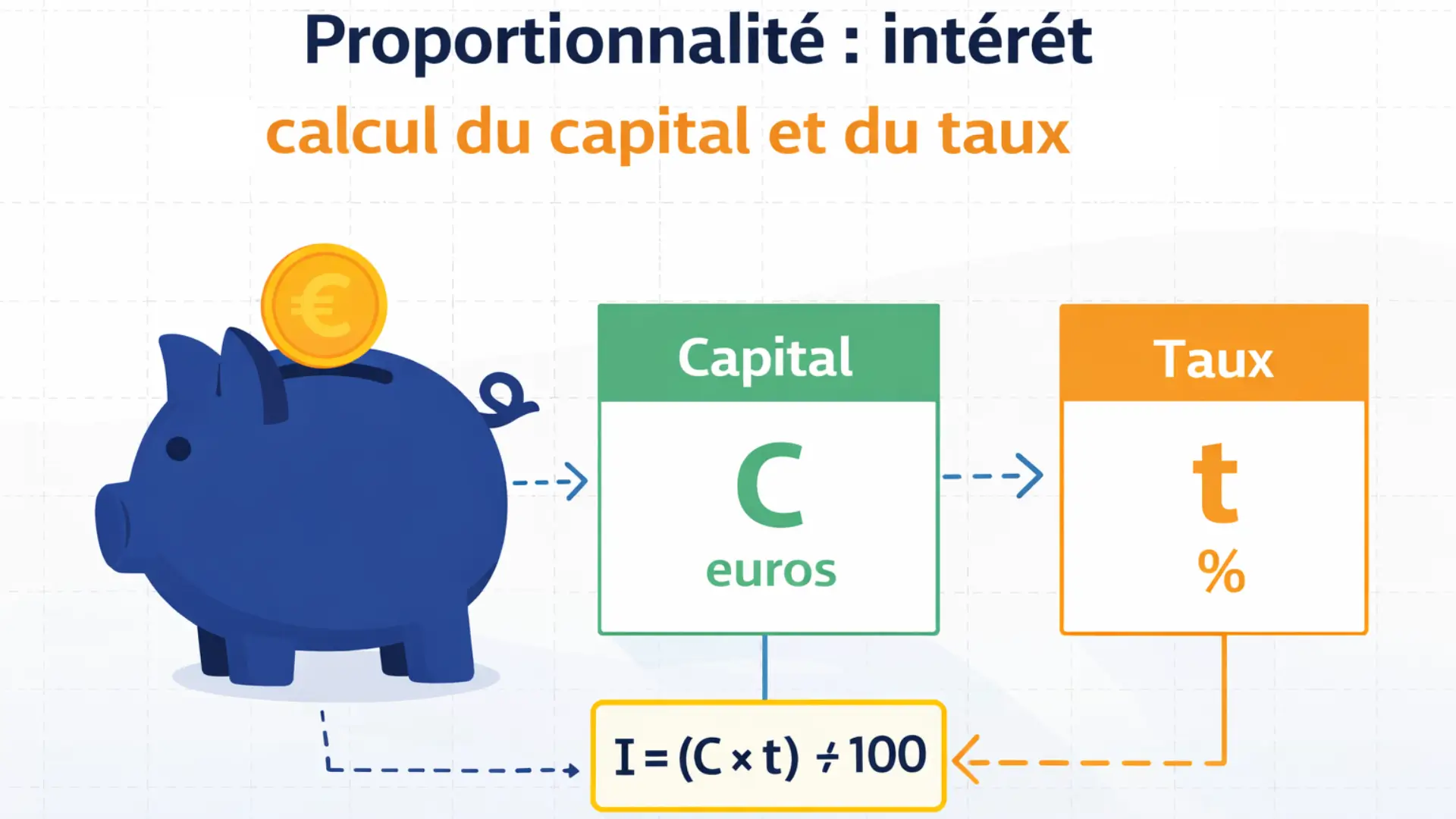
Le capital est la somme d’argent placée au départ dans une banque. On le note généralement C. Par exemple, si une personne place 32 000 euros, alors le capital est C = 32 000 €.
Le taux est un pourcentage qui indique ce que rapporte le capital en une année. Il est noté t et s’exprime en pourcentage. Un taux de 2,5 % signifie que, pour 100 euros placés, on gagne 2,5 euros en une année.
L’intérêt est la somme d’argent gagnée grâce au placement du capital pendant une année. On le note I annuel. L’intérêt dépend du capital et du taux, ce qui montre qu’il existe une relation de proportionnalité entre ces grandeurs.
Calculer l’intérêt annuel à l’aide de la proportionnalité
Lorsque l’on place un capital dans une banque pendant une année, l’intérêt obtenu est proportionnel au capital et au taux appliqué. Cela signifie que plus le capital est grand, plus l’intérêt est important, et plus le taux est élevé, plus le gain augmente.
Pour calculer l’intérêt annuel, on utilise la relation de proportionnalité suivante :
L’intérêt annuel est égal au capital multiplié par le taux, puis divisé par 100.
On écrit la formule :
I annuel = (C × t) ÷ 100
où
C représente le capital
t représente le taux en pourcentage
I annuel représente l’intérêt obtenu en une année
Exemple expliqué
La mère de Rim place un capital de 32 000 euros dans une banque au taux de 2,5 % pendant une année.
Le capital est C = 32 000 €
Le taux est t = 2,5 %
On applique la formule :
I annuel = (32 000 × 2,5) ÷ 100
I annuel = 80 000 ÷ 100
I annuel = 800 €
Cela signifie qu’au bout d’une année, le capital rapporte un intérêt de 800 euros.
Cette situation montre clairement la proportionnalité entre le capital et l’intérêt : si le capital double, l’intérêt double également, à taux constant.
Déterminer le capital à partir de l’intérêt
Dans certaines situations, on connaît l’intérêt annuel obtenu et le taux appliqué, mais on cherche le capital placé au départ. Comme il s’agit d’une situation de proportionnalité, on peut utiliser la relation entre le capital, le taux et l’intérêt.
On part de la formule de l’intérêt annuel :
I annuel = (C × t) ÷ 100
Pour trouver le capital, on transforme cette relation :
C = (I annuel × 100) ÷ t
où
C est le capital
I annuel est l’intérêt obtenu en une année
t est le taux en pourcentage
Exemple expliqué
Aya obtient un intérêt annuel de 3 600 euros après avoir placé son argent à un taux de 4 %.
L’intérêt annuel est I = 3 600 €
Le taux est t = 4 %
On applique la formule :
C = (3 600 × 100) ÷ 4
C = 360 000 ÷ 4
C = 90 000 €
Le capital placé par Sarah est donc de 90 000 euros.
Ce calcul montre que le capital est proportionnel à l’intérêt lorsque le taux est fixé.
Calculer le taux à partir du capital et de l’intérêt
Il arrive que l’on connaisse le capital placé et l’intérêt obtenu après une année, mais que le taux ne soit pas donné. Dans ce cas, on utilise encore une situation de proportionnalité entre le capital et l’intérêt.
On part de la formule de l’intérêt annuel :
I annuel = (C × t) ÷ 100
Pour déterminer le taux, on transforme la formule :
t = (I annuel × 100) ÷ C
où
t est le taux en pourcentage
I annuel est l’intérêt obtenu en une année
C est le capital placé
Exemple expliqué
Ayoub place un capital de 48 000 euros dans une banque. Après une année, il obtient un intérêt de 1 440 euros.
Le capital est C = 48 000 €
L’intérêt annuel est I = 1 440 €
On calcule le taux :
t = (1 440 × 100) ÷ 48 000
t = 144 000 ÷ 48 000
t = 3
Le taux de placement est donc de 3 %.
Ce calcul confirme que, pour un capital donné, l’intérêt est proportionnel au taux appliqué.
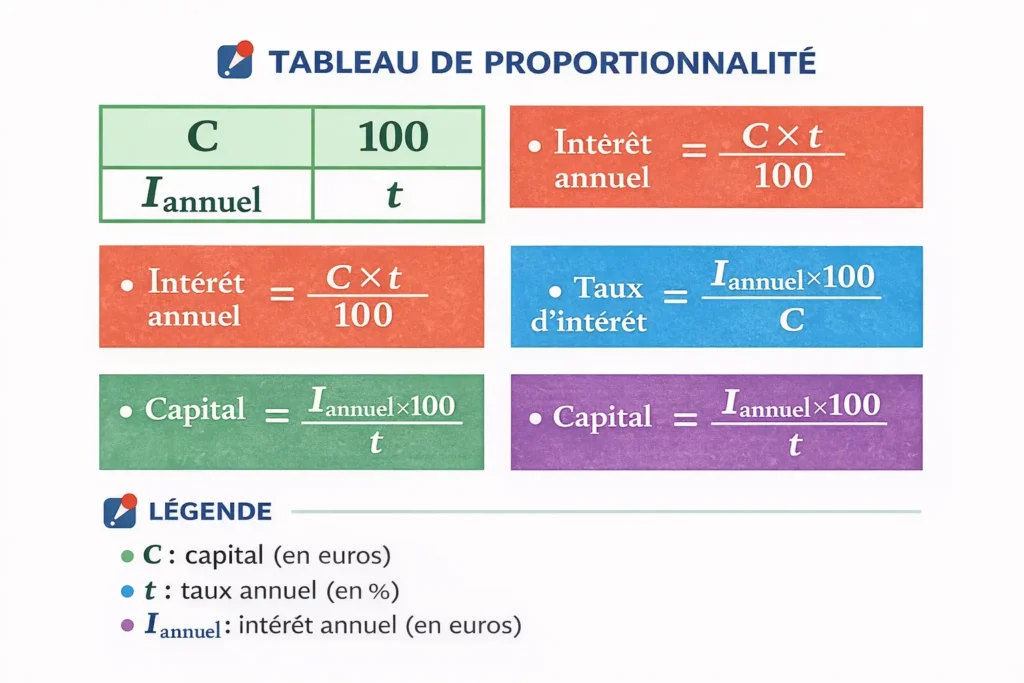
Synthèse des formules de la proportionnalité
capital, taux et intérêt
Dans les situations de proportionnalité liées aux placements d’argent, trois grandeurs interviennent : le capital, le taux et l’intérêt annuel. Ces trois grandeurs sont liées entre elles par des formules simples.
Formule de l’intérêt annuel
Lorsque le capital et le taux sont connus, l’intérêt annuel se calcule par la formule :
I annuel = (C × t) ÷ 100
Cette formule permet de calculer le gain obtenu après une année.
Formule du capital
Lorsque l’intérêt annuel et le taux sont connus, le capital se calcule par la formule :
C = (I annuel × 100) ÷ t
Cette formule permet de retrouver la somme placée au départ.
Formule du taux
Lorsque le capital et l’intérêt annuel sont connus, le taux se calcule par la formule :
t = (I annuel × 100) ÷ C
Cette formule permet de déterminer le pourcentage appliqué au capital.
À retenir
Dans toutes ces situations, il existe une relation de proportionnalité entre le capital, le taux et l’intérêt. Modifier l’une de ces grandeurs entraîne une modification proportionnelle des autres, lorsque les conditions restent les mêmes.
La maîtrise de ces trois formules permet de résoudre facilement les exercices et les problèmes liés à la proportionnalité dans la vie quotidienne.
Exemples récapitulatifs
Exemple 1 Calcul de l’intérêt annuel
Un capital de 25 000 euros est placé à un taux de 3 % pendant une année.
Calculer l’intérêt annuel.
Le capital est C = 25 000 €
Le taux est t = 3 %
I annuel = (25 000 × 3) ÷ 100
I annuel = 75 000 ÷ 100
I annuel = 750 €
L’intérêt annuel est de 750 euros.
Exemple 2 Calcul du capital
Un intérêt annuel de 1 200 euros est obtenu à un taux de 4 %.
Calculer le capital placé.
L’intérêt annuel est I = 1 200 €
Le taux est t = 4 %
C = (1 200 × 100) ÷ 4
C = 120 000 ÷ 4
C = 30 000 €
Le capital placé est de 30 000 euros.
Exemple 3 Calcul du taux
Un capital de 40 000 euros rapporte un intérêt annuel de 2 000 euros.
Calculer le taux appliqué.
Le capital est C = 40 000 €
L’intérêt annuel est I = 2 000 €
t = (2 000 × 100) ÷ 40 000
t = 200 000 ÷ 40 000
t = 5
Le taux de placement est de 5 %.
Exercices d’application
Exercice 1 Calculer l’intérêt annuel
1 Un capital de 18 000 euros est placé à un taux de 2 %.
2 Un capital de 35 000 euros est placé à un taux de 4 %.
Calculer l’intérêt annuel dans chaque cas.
Exercice 2 Calculer le capital
1 Un intérêt annuel de 900 euros est obtenu à un taux de 3 %.
2 Un intérêt annuel de 2 500 euros est obtenu à un taux de 5 %.
Calculer le capital placé dans chaque cas.
Exercice 3 Calculer le taux
1 Un capital de 20 000 euros rapporte un intérêt annuel de 600 euros.
2 Un capital de 50 000 euros rapporte un intérêt annuel de 2 000 euros.
Calculer le taux dans chaque situation.
Exercice 4 Situation problème
Un capital est placé à un taux de 4 %. Après une année, l’intérêt obtenu est de 1 600 euros.
1 Calculer le capital placé.
2 Vérifier le résultat à l’aide de la formule de l’intérêt.
Erreurs fréquentes
Dans les exercices de proportionnalité liés au capital, au taux et à l’intérêt, certaines erreurs reviennent souvent. Les connaître permet de mieux les éviter.
Confondre le capital et l’intérêt.
Le capital est la somme d’argent placée au départ, alors que l’intérêt est la somme gagnée après une année.
Oublier de diviser par 100 lors du calcul de l’intérêt ou du taux.
Le taux étant exprimé en pourcentage, la division par 100 est indispensable.
Utiliser une mauvaise formule.
Chaque situation nécessite une formule précise selon ce que l’on cherche à calculer.
Mal identifier les données de l’énoncé.
Ne pas repérer correctement le capital, le taux ou l’intérêt peut conduire à une erreur de calcul.
Ne pas vérifier la cohérence du résultat.
Un intérêt très élevé par rapport au capital doit alerter l’élève sur une éventuelle erreur.
Oublier l’unité monétaire dans la réponse.
Une réponse sans euros ou sans pourcentage est incomplète.
Conseils pour les profs et les parents
La notion de proportionnalité appliquée au capital, au taux et à l’intérêt est plus facile à comprendre lorsqu’elle est reliée à des situations concrètes.
Conseils pour les profs
Il est conseillé de partir d’exemples proches de la vie quotidienne, comme l’épargne ou les placements bancaires simples. Utiliser des tableaux de proportionnalité aide les élèves à visualiser la relation entre le capital et l’intérêt.
Faire écrire systématiquement la formule avant le calcul permet de structurer la démarche et d’éviter les erreurs. Encourager les élèves à expliquer oralement leur raisonnement renforce la compréhension.
Il est également utile de varier les exercices en proposant des calculs directs et des situations problèmes.
Conseils pour les parents
À la maison, on peut aider l’enfant en lui demandant d’expliquer ce que représentent le capital, le taux et l’intérêt avec ses propres mots. Relier les exercices à des situations simples, comme l’épargne familiale, facilite la compréhension.
Il est important d’encourager l’enfant à vérifier ses résultats et à ne pas oublier la division par 100 lors des calculs. L’objectif est de comprendre la méthode plutôt que de mémoriser uniquement les formules.
Mot du prof
La proportionnalité entre le capital, le taux et l’intérêt est une notion importante qui permet de comprendre comment évolue une somme d’argent avec le temps. En maîtrisant ces relations, tu pourras résoudre facilement de nombreux problèmes de la vie quotidienne.
Prends toujours le temps d’identifier les données de l’énoncé, d’écrire la formule correcte et de vérifier ton résultat. La rigueur et la méthode sont les clés de la réussite en mathématiques.
Avec de l’entraînement, ces calculs deviendront simples et naturels. Chaque exercice est une occasion de progresser et de gagner en confiance.
Télécharger les exercices en PDF
Pour s’entraîner davantage et consolider la leçon, vous pouvez télécharger le PDF d’exercices sur la proportionnalité (capital, taux et intérêt). Ce document contient un rappel de cours, des exemples récapitulatifs et des exercices progressifs pour appliquer les formules vues en classe. Il est adapté au travail en classe, à la révision à la maison et à la préparation des évaluations.
Conclusion
Dans cette leçon sur la proportionnalité : intérêt, nous avons appris à calculer l’intérêt, le capital et le taux à l’aide de formules simples. Les exemples et les exercices permettent de mieux comprendre des situations concrètes liées à l’argent et à l’épargne.
Pour réviser autrement, des rappels et des exercices sont également partagés sur Pinterest. Ils peuvent être enregistrés ou partagés afin de faciliter la révision et l’entraînement.
Ces connaissances constituent une base importante pour les apprentissages futurs en mathématiques, notamment dans l’étude des pourcentages et des situations de proportionnalité plus avancées.
FAQ : proportionnalité : intérêt
Qu’est-ce que la proportionnalité ?
Deux grandeurs sont proportionnelles lorsque l’une augmente ou diminue dans le même rapport que l’autre. Dans cette leçon, le capital, le taux et l’intérêt sont liés par une relation de proportionnalité.
Que représente le capital ?
Le capital est la somme d’argent placée au départ dans une banque. C’est la valeur de départ utilisée pour les calculs.
Que signifie le taux ?
Le taux est un pourcentage qui indique combien rapporte un capital pour 100 unités en une année. Il permet de calculer l’intérêt.
Qu’est-ce que l’intérêt annuel ?
L’intérêt annuel est la somme d’argent gagnée après une année grâce au placement du capital à un certain taux.
Pourquoi divise -t-on par 100 dans les formules ?
Parce que le taux est exprimé en pourcentage. Diviser par 100 permet de passer du pourcentage à une valeur utilisable dans le calcul.
Comment savoir quelle formule utiliser ?
Il faut identifier ce que l’on connaît et ce que l’on cherche.
Si on cherche l’intérêt, on utilise la formule de l’intérêt.
Si on cherche le capital ou le taux, on utilise la formule correspondante.
Faut-il toujours écrire l’unité dans la réponse ?
Oui. Une réponse doit toujours contenir l’unité monétaire, comme le dirham, ou le pourcentage pour le taux.