La proportionnalité : la masse volumique est une notion essentielle en mathématiques et en sciences. Elle permet de comprendre le lien entre la masse et le volume d’une matière, qu’elle soit liquide ou solide.
Pourquoi deux objets de même volume peuvent-ils avoir des masses différentes ? Comment calculer la masse ou le volume à partir d’une masse volumique donnée ?
Dans ce cours clair, tu vas découvrir pas à pas la masse volumique, comprendre pourquoi il s’agit d’une situation de proportionnalité, apprendre à utiliser les formules, lire des tableaux et des graphiques, puis t’entraîner avec des exercices corrigés pour bien maîtriser la méthode.
Table of Contents
Découverte : masse, volume et proportionnalité
On a représenté sur un graphique la masse en grammes d’un objet en fonction de son volume en centimètres cubes.
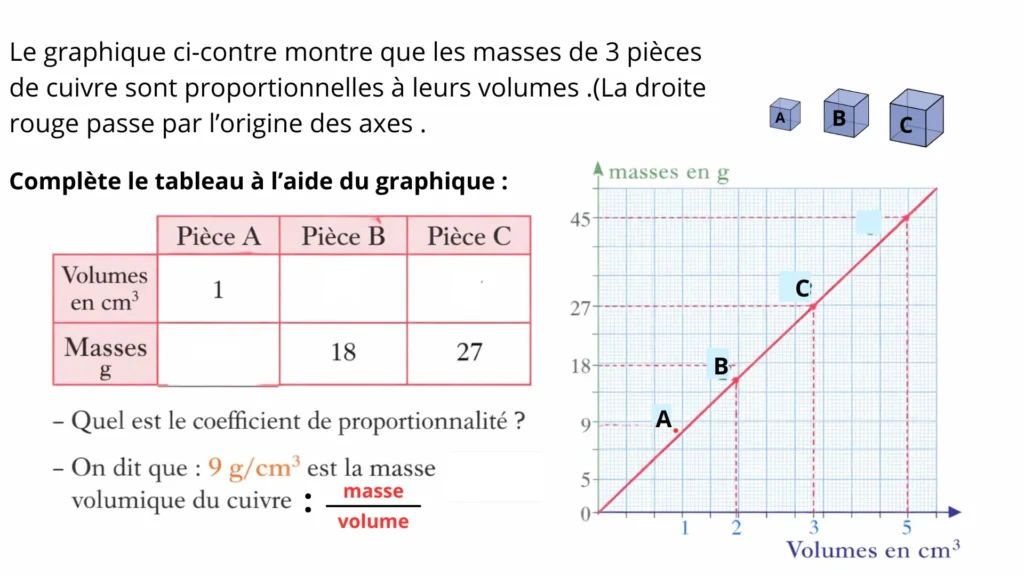
1. Lecture du graphique
L’axe horizontal représente le volume.
L’axe vertical représente la masse.
Les points du graphique sont alignés.
La droite passe par l’origine du repère (0 ; 0).
Cela signifie que lorsque le volume est nul, la masse est également nulle.
2. Mise en évidence de la proportionnalité
Lorsque le volume double, la masse double.
Lorsque le volume triple, la masse triple.
La masse varie proportionnellement au volume.
Il s’agit donc d’une situation de proportionnalité.
3. Compléter le tableau correspondant
À partir du graphique, on peut lire plusieurs couples de valeurs volume et masse et compléter un tableau de proportionnalité.
À chaque volume correspond une masse bien déterminée.
Le rapport entre la masse et le volume reste constant.
4. Recherche du coefficient de proportionnalité
Pour déterminer le coefficient de proportionnalité, on calcule le rapport de la masse sur le volume.
coefficient = masse ÷ volume
Quel que soit le point choisi sur le graphique, on obtient la même valeur.
Ce coefficient est appelé la masse volumique du liquide.
5. Conclusion de la découverte
La masse volumique permet de relier la masse et le volume d’une matière.
Dans une situation de proportionnalité, la masse est proportionnelle au volume et le coefficient de proportionnalité correspond à la masse volumique.
On peut maintenant définir précisément la masse volumique et apprendre à la calculer.
Apprends : définition de la masse volumique
La masse volumique d’une matière permet de connaître la masse correspondant à un volume donné de cette matière.
La masse volumique est le rapport entre la masse et le volume.
On la note généralement par la lettre grecque ρ (rho).
masse volumique = masse ÷ volume
Cela signifie que, pour une même matière, la masse est proportionnelle au volume.
Interprétation
La masse volumique indique la masse d’un centimètre cube ou d’un mètre cube de matière.
Par exemple, si une matière a une masse volumique élevée, cela signifie qu’un petit volume de cette matière a une masse importante.
Inversement, une matière de faible masse volumique est plus légère pour un même volume.
Lien avec la proportionnalité
Dans une situation de proportionnalité entre la masse et le volume, la masse volumique est le coefficient de proportionnalité.
Elle permet de passer du volume à la masse et inversement.
Voici la partie Les formules à connaître, rédigée de façon claire, simple et directement exploitable par les élèves.
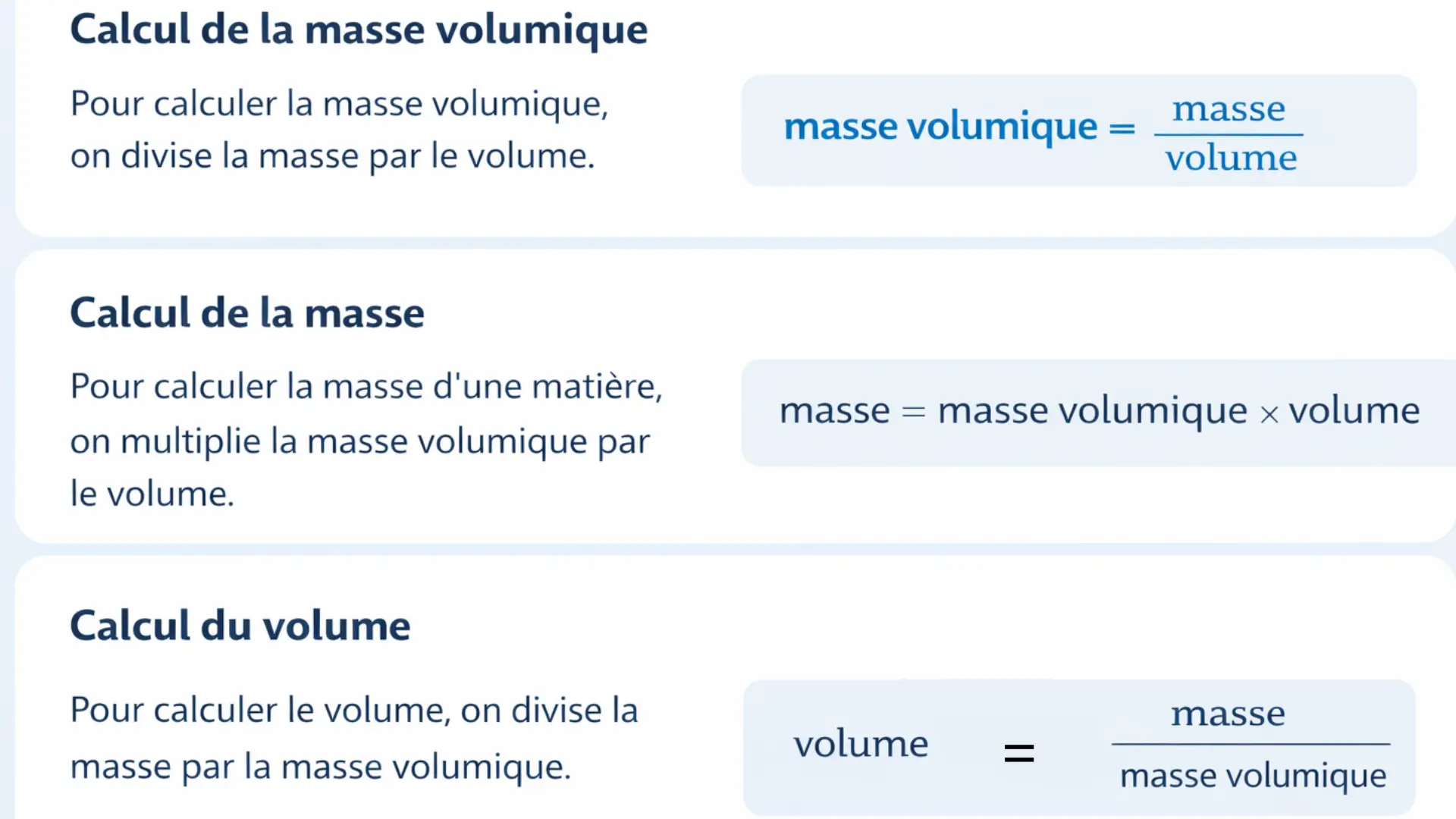
Les formules à connaître
La masse, le volume et la masse volumique sont liés par une relation de proportionnalité.
On utilise les formules suivantes selon la grandeur recherchée.
Calcul de la masse volumique
Pour calculer la masse volumique, on divise la masse par le volume.
masse volumique = masse ÷ volume
Calcul de la masse
Pour calculer la masse d’une matière, on multiplie la masse volumique par le volume.
masse = masse volumique × volume
Calcul du volume
Pour calculer le volume, on divise la masse par la masse volumique.
volume = masse ÷ masse volumique
Remarque importante
Avant d’appliquer une formule, il est indispensable de vérifier que les unités sont compatibles.
Une erreur d’unité entraîne un résultat faux.
Les unités de la masse volumique
La masse volumique est le rapport entre une masse et un volume.
Son unité dépend donc des unités utilisées pour la masse et le volume.
Unités courantes
On utilise principalement les unités suivantes :
- le gramme par centimètre cube
g/cm³ - le kilogramme par décimètre cube
kg/dm³ - la tonne par mètre cube
t/m³
Correspondances importantes
Certaines unités sont équivalentes :
1 g/cm³ = 1 kg/dm³
Cette égalité est très utilisée, notamment pour les liquides.
Exemple
La masse volumique de l’eau est égale à :
1 g/cm³
ou
1 kg/dm³
Cela signifie qu’un centimètre cube d’eau a une masse de 1 gramme et qu’un décimètre cube d’eau a une masse de 1 kilogramme.
Attention aux unités
Avant d’effectuer un calcul, il est indispensable de vérifier que les unités de la masse et du volume sont compatibles avec l’unité de la masse volumique utilisée.
Une erreur d’unité conduit toujours à un résultat faux.
Proportionnalité : tableau masse – volume
La masse et le volume d’une matière sont liés par une situation de proportionnalité.
La masse volumique est le coefficient de proportionnalité entre la masse et le volume.
Construction du tableau de proportionnalité
On place le volume sur la première ligne et la masse sur la deuxième ligne.
Le tableau permet de relier directement les valeurs correspondantes.
Exemple :
| Volume (cm³) | 1 | 2 | 3 | 5 |
|---|---|---|---|---|
| Masse (g) | 8 | 16 | 24 | 40 |
Lecture du tableau
On observe que :
- lorsque le volume double, la masse double ;
- lorsque le volume triple, la masse triple.
La masse est donc proportionnelle au volume.
Coefficient de proportionnalité
Pour déterminer le coefficient de proportionnalité, on calcule le rapport de la masse sur le volume.
coefficient = masse ÷ volume
Application au tableau
Dans le tableau précédent :
8 ÷ 1 = 16 ÷ 2 = 24 ÷ 3 = 8
Le coefficient de proportionnalité est donc égal à 8.
Ce coefficient correspond à la masse volumique de la matière, exprimée en g/cm³.
Utilisation du tableau
Le tableau de proportionnalité permet :
- de calculer une masse à partir d’un volume ;
- de calculer un volume à partir d’une masse ;
- de vérifier qu’il s’agit bien d’une situation de proportionnalité.
Représentation graphique
La relation entre la masse et le volume peut être représentée par un graphique.
Axes du graphique
On place :
- le volume sur l’axe horizontal ;
- la masse sur l’axe vertical.
Chaque point du graphique représente un couple de valeurs volume et masse.
Droite de proportionnalité
Lorsque la masse est proportionnelle au volume, les points du graphique sont alignés sur une droite.
Cette droite :
- passe par l’origine du repère (0 ; 0) ;
- représente une situation de proportionnalité.
Interprétation du graphique
Plus le volume augmente, plus la masse augmente de façon régulière.
La pente de la droite dépend de la masse volumique de la matière.
Une droite plus inclinée correspond à une masse volumique plus élevée.
Lecture d’un point du graphique
Pour lire un point du graphique :
- on repère sa position sur l’axe des volumes ;
- on lit la masse correspondante sur l’axe des masses.
Le graphique permet ainsi de déterminer rapidement la masse associée à un volume donné, ou inversement.
Exercices d’application : proportionnalité et masse volumique
Exercice 1
Un solide a une masse de 450 g et un volume de 50 cm³.
- Vérifie s’il s’agit d’une situation de proportionnalité entre la masse et le volume.
- Calcule la masse volumique de ce solide.
- Précise l’unité de la masse volumique obtenue.
Exercice 2
La masse volumique d’un métal est 7,8 g/cm³.
- Calcule la masse de ce métal pour un volume de 10 cm³.
- Quelle serait la masse pour un volume de 25 cm³ ?
Exercice 3
On considère le tableau suivant :
| Volume (cm³) | 2 | 4 | 6 | 10 |
|---|---|---|---|---|
| Masse (g) | 16 | … | … | … |
- Complète le tableau.
- Détermine le coefficient de proportionnalité.
- Que représente ce coefficient ?
Exercice 4
Un liquide a une masse volumique de 1,2 g/cm³.
- Calcule la masse correspondant à un volume de 15 cm³.
- Calcule le volume correspondant à une masse de 36 g.
Exercice 5
On représente graphiquement la masse en fonction du volume pour une matière donnée.
- Explique pourquoi la droite passe par l’origine du repère.
- Indique ce que représente la pente de la droite.
- Que peut-on dire de la relation entre la masse et le volume ?
Exercice 6
La masse volumique de l’eau est 1 g/cm³.
- Quelle est la masse de 8 cm³ d’eau ?
- Quel est le volume correspondant à une masse de 250 g d’eau ?
Télécharger le PDF : Exercices corrigés sur la masse volumique
Pour t’entraîner et mieux maîtriser la proportionnalité : la masse volumique, un PDF à télécharger gratuitement est mis à ta disposition.
Ce document contient :
- des exercices d’application variés sur la masse volumique ;
- une progression adaptée au niveau CM2 / 6e ;
- un corrigé détaillé pour vérifier tes réponses et comprendre la méthode ;
- un format prêt à imprimer ou à utiliser à la maison.
Télécharger le PDF des exercices avec correction :
Ce PDF est particulièrement utile pour :
- réviser avant un contrôle .
- s’entraîner en autonomie .
- accompagner les élèves à la maison .
- proposer un support clé en main en classe.
Erreurs fréquentes
Lors de l’étude de la proportionnalité : la masse volumique, certaines erreurs reviennent souvent. Les identifier permet de les éviter.
Confondre masse et volume
La masse et le volume sont deux grandeurs différentes.
La masse s’exprime en grammes ou en kilogrammes, tandis que le volume s’exprime en centimètres cubes, décimètres cubes ou mètres cubes.
Se tromper de formule
Il arrive de diviser au lieu de multiplier, ou inversement.
Avant de calculer, il faut toujours se demander quelle grandeur on cherche et écrire la formule correspondante.
Oublier ou mélanger les unités
Utiliser des unités incompatibles conduit à un résultat faux.
Il est indispensable de vérifier que la masse, le volume et la masse volumique sont exprimés dans des unités cohérentes.
Ne pas reconnaître une situation de proportionnalité
Si la masse est proportionnelle au volume, le graphique doit être une droite passant par l’origine.
Si ce n’est pas le cas, il ne s’agit pas d’une situation de proportionnalité.
Mauvaise lecture d’un tableau ou d’un graphique
Une erreur de lecture sur un tableau de proportionnalité ou sur un graphique entraîne une erreur de calcul.
Il faut toujours prendre le temps de lire correctement les valeurs avant de calculer.
Ne pas vérifier la cohérence du résultat
Un résultat trop grand ou trop petit doit alerter.
Il est important de vérifier si le résultat est logique par rapport à la situation étudiée.
Astuces et méthode rapide
Pour réussir les exercices sur la proportionnalité : la masse volumique, il est important d’adopter une méthode simple et efficace.
Étape 1 : Identifier ce que l’on cherche
Avant de calculer, il faut repérer la grandeur demandée dans l’énoncé.
S’agit-il de la masse, du volume ou de la masse volumique ?
Étape 2 : Écrire la formule adaptée
Une fois la grandeur identifiée, on choisit la formule correspondante.
Écrire la formule avant de calculer permet d’éviter les erreurs.
Étape 3 : Vérifier les unités
Les unités doivent être compatibles entre elles.
Si ce n’est pas le cas, il faut d’abord les convertir.
Étape 4 : Effectuer le calcul
On applique la formule correctement en respectant l’ordre des opérations.
Étape 5 : Vérifier le résultat
On se demande si le résultat est logique.
Une masse volumique très élevée ou très faible doit alerter.
Astuce importante
Lorsque la masse et le volume sont liés par une situation de proportionnalité, il est souvent utile de passer par un tableau de proportionnalité avant d’utiliser directement les formules.
Conseils pour les parents
La notion de masse volumique peut sembler abstraite au premier abord, mais elle devient plus facile à comprendre lorsqu’elle est reliée à des situations concrètes.
Utiliser des exemples du quotidien
À la maison, il est possible de comparer des objets de même volume mais de masses différentes, comme une bouteille d’eau et une bouteille d’huile.
Cela aide l’enfant à comprendre que toutes les matières n’ont pas la même masse pour un même volume.
Encourager la méthode avant le calcul
Avant de calculer, invitez votre enfant à dire à voix haute ce qu’il cherche et à écrire la formule correspondante.
Cette habitude permet d’éviter de nombreuses erreurs.
Vérifier les unités ensemble
Prenez le temps de vérifier avec votre enfant les unités utilisées dans les exercices.
Insister sur la cohérence des unités aide à mieux comprendre les résultats.
Réviser par petites séances
Des révisions courtes et régulières sont plus efficaces qu’un long travail ponctuel.
Cinq à dix minutes suffisent pour revoir une formule ou refaire un exercice simple.
Utiliser le PDF d’exercices corrigés
Le PDF proposé dans cet article permet à votre enfant de s’entraîner en autonomie.
Les corrections l’aident à comprendre ses erreurs et à progresser à son rythme.
Conseils pour l’enseignant(e)
La masse volumique est une notion transversale qui permet de renforcer la compréhension de la proportionnalité tout en faisant le lien avec les sciences physiques.
Partir d’une situation concrète
Il est recommandé de commencer par une situation de découverte à partir d’un graphique ou d’un tableau reliant la masse et le volume.
Cela permet aux élèves d’identifier eux-mêmes la situation de proportionnalité avant d’introduire la définition formelle.
Insister sur le coefficient de proportionnalité
Mettre en évidence que la masse volumique correspond au coefficient de proportionnalité entre la masse et le volume aide les élèves à donner du sens aux formules.
Cette étape est essentielle pour éviter un apprentissage purement mécanique.
Varier les supports
Alterner entre tableau de proportionnalité, graphique et calcul littéral permet de toucher différents profils d’élèves et de renforcer la compréhension globale de la notion.
Différencier les activités
Pour les élèves en difficulté, privilégier des tableaux simples avec des nombres entiers.
Pour les élèves plus à l’aise, proposer des situations avec des conversions d’unités ou une interprétation graphique plus fine.
Favoriser la verbalisation
Inviter les élèves à expliquer leur raisonnement à l’oral ou à l’écrit permet de repérer les erreurs de compréhension et de consolider les acquis.
Utiliser le PDF comme support pédagogique
Le PDF d’exercices avec correction peut être utilisé pour le travail en autonomie, les devoirs à la maison ou la remédiation en classe.
Mot du prof
La masse volumique peut paraître difficile au début, mais il faut se rappeler qu’il s’agit avant tout d’une situation de proportionnalité, comme celles que tu connais déjà.
En prenant le temps de bien comprendre le lien entre la masse et le volume, d’écrire les formules correctement et de vérifier les unités, tu verras que les calculs deviennent simples et logiques.
N’hésite pas à t’entraîner régulièrement avec les exercices proposés et à utiliser le tableau de proportionnalité comme outil de vérification. Avec un peu de méthode et de pratique, cette notion sera vite maîtrisée.
Conclusion
Pour mieux mémoriser la proportionnalité : la masse volumique et retrouver facilement ce cours clair et ses exercices corrigés, pense à enregistrer cette leçon sur Pinterest afin de la consulter plus tard.
FAQ ( Proportionnalité : la masse volumique )
Qu’est-ce que la masse volumique
La masse volumique est le rapport entre la masse et le volume d’une matière. Elle permet de savoir quelle masse correspond à un volume donné.
Quelle est la formule de la masse volumique
La masse volumique se calcule en divisant la masse par le volume.
Masse volumique = masse ÷ volume.
Comment calculer la masse à partir de la masse volumique
Pour calculer la masse, on multiplie la masse volumique par le volume.
Masse = masse volumique × volume.
Comment calculer le volume
Pour calculer le volume, on divise la masse par la masse volumique.
Volume = masse ÷ masse volumique.
Quelles sont les unités de la masse volumique
Les unités les plus utilisées sont le g/cm³, le kg/dm³ et le t/m³.
Pourquoi la droite passe-t-elle par l’origine du repère
La droite passe par l’origine car lorsque le volume est nul, la masse est également nulle. Cela caractérise une situation de proportionnalité.
Comment savoir s’il s’agit d’une situation de proportionnalité
Il s’agit d’une situation de proportionnalité si le rapport masse ÷ volume est constant et si la représentation graphique est une droite passant par l’origine.
Pourquoi faut-il vérifier les unités avant de calculer
Des unités incompatibles donnent un résultat faux. Vérifier les unités permet d’éviter les erreurs de calcul.