Proportionnalité : l’échelle d’un plan est une notion essentielle pour comprendre comment représenter une distance réelle sur un plan ou sur une carte tout en respectant les proportions. Cette notion de proportionnalité permet de passer facilement d’une mesure dessinée à une mesure réelle, et inversement, à condition de bien interpréter l’échelle indiquée.
Dans cette leçon, la proportionnalité : l’échelle d’un plan est utilisée pour apprendre à effectuer des calculs précis, déterminer une distance réelle à partir d’un plan, calculer une distance sur une carte et résoudre des situations concrètes issues de la cartographie et de la vie quotidienne. Grâce à des exemples simples, des exercices progressifs et une méthode claire, l’élève pourra maîtriser la proportionnalité : l’échelle d’un plan et l’appliquer efficacement dans des contextes scolaires et pratiques.
Table of Contents
L’échelle d’un plan
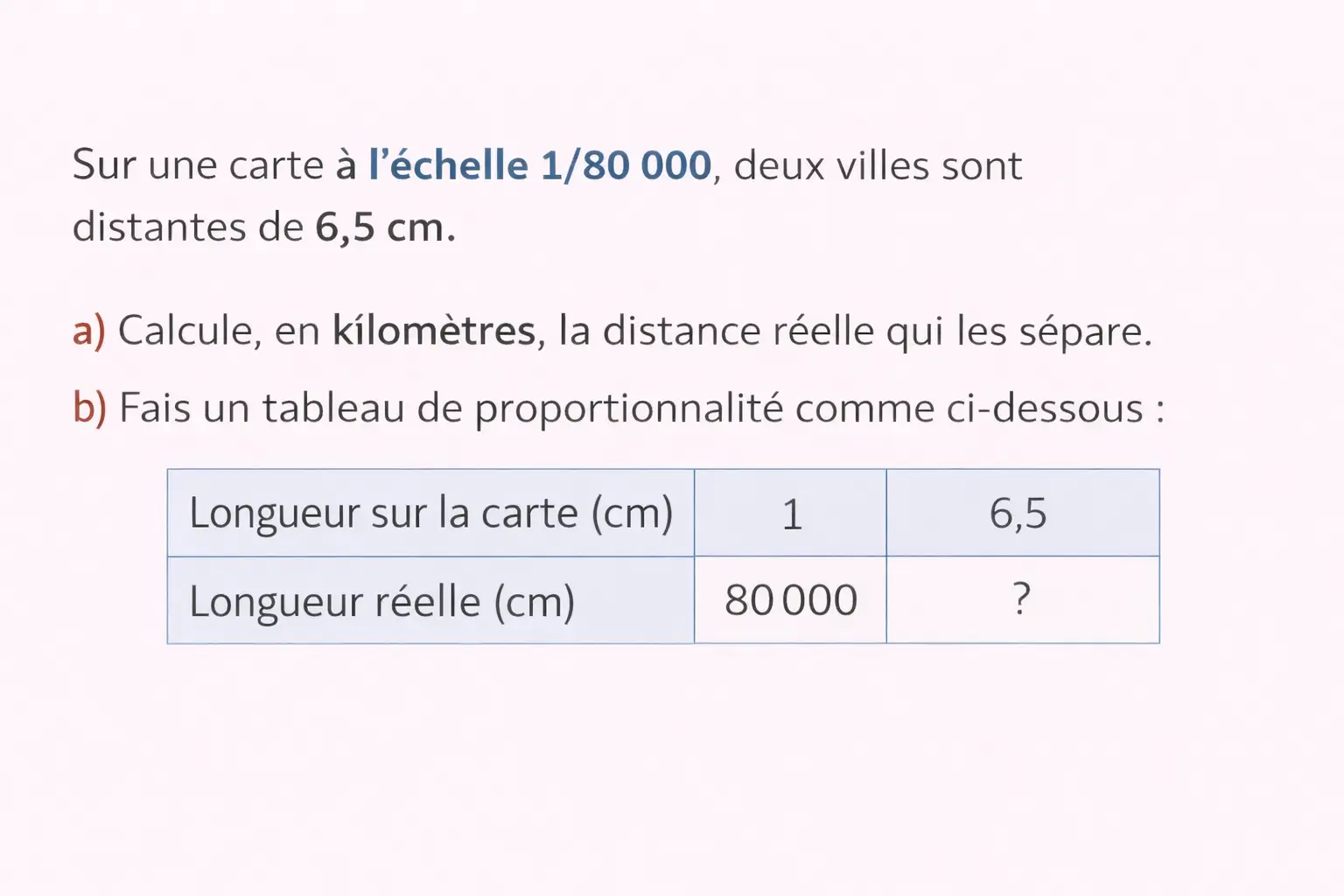
Une échelle permet de représenter une distance réelle sur un plan ou sur une carte en respectant la proportionnalité. Elle indique le lien entre une longueur mesurée sur le plan et la longueur correspondante dans la réalité.
L’échelle est le plus souvent écrite sous la forme d’une fraction dont le numérateur est 1, par exemple 1 : 25 000 ou 1/25 000.
Cela signifie que 1 cm sur le plan représente 25 000 cm dans la réalité.
Pour utiliser correctement une échelle, il est indispensable que les distances sur le plan et les distances réelles soient exprimées dans la même unité, généralement le centimètre. C’est pourquoi il faut souvent convertir les mètres ou les kilomètres en centimètres avant de faire les calculs.
L’échelle est utilisée dans de nombreuses situations comme la lecture d’une carte géographique, l’étude d’un plan de maison ou la mesure de distances entre deux villes. Comprendre l’échelle d’un plan permet donc de passer correctement du dessin à la réalité.
Calculer la distance réelle à partir d’un plan
Dans la proportionnalité : l’échelle d’un plan, on cherche parfois à connaître la distance réelle correspondant à une distance mesurée sur un plan ou sur une carte.
Pour cela, on utilise l’échelle et un tableau de proportionnalité, en commençant toujours par 1 cm sur le plan.
Exemple
Sur une carte à l’échelle 1 : 25 000, la distance mesurée entre deux points est de 8 cm.
On sait que :
1 cm sur le plan → 25 000 cm dans la réalité
Pour expliquer le passage à 8 cm, on écrit :
1 cm sur le plan → 8 cm sur le plan
(ce qui signifie que l’on passe de la référence 1 cm à la distance réellement mesurée sur le plan, qui est 8 cm)
On applique alors la même proportion à la distance réelle.
25 000 cm → 8 × 25 000 cm = 200 000 cm
La distance réelle est donc 200 000 cm.
On termine par la conversion :
200 000 cm = 2 km
La distance réelle entre ces deux points est donc 2 km.

Calculer la distance sur un plan à partir de la distance réelle
Dans la proportionnalité : l’échelle d’un plan, on peut connaître la distance réelle entre deux lieux et chercher la distance correspondante sur le plan ou sur la carte.
On commence toujours par convertir la distance réelle en centimètres, puis on utilise l’échelle.
Exemple
La distance réelle entre deux villes est de 2 000 km.
La carte est à l’échelle 1 : 4 000 000.
On convertit la distance réelle en centimètres.
2 000 km = 200 000 000 cm
On sait que :
1 cm sur le plan → 4 000 000 cm dans la réalité
On compare maintenant la distance réelle de référence à la distance réelle donnée.
4 000 000 cm → 200 000 000 cm
(cela signifie que l’on passe de la distance réelle correspondant à 1 cm sur le plan à la distance réelle donnée dans l’énoncé)
Pour passer de 4 000 000 cm à 200 000 000 cm, on multiplie par 50.
On applique exactement la même opération sur le plan.
1 cm sur le plan → 50 cm sur le plan
(c’est la distance mesurée sur le plan correspondant à la distance réelle donnée)
La distance sur le plan est donc 50 cm.
À retenir
Pour calculer la distance sur un plan, on divise la distance réelle par le nombre de l’échelle, après avoir converti les unités, puis on applique la proportion.
Déterminer l’échelle d’un plan
Dans la proportionnalité : l’échelle d’un plan, il arrive que l’échelle ne soit pas indiquée. On connaît seulement une distance sur le plan et la distance réelle correspondante. Il faut alors déterminer l’échelle du plan.
Pour cela, on commence toujours par mettre les deux distances dans la même unité, généralement le centimètre, puis on utilise un raisonnement de proportionnalité.
Exemple
Sur une carte, une rue de longueur réelle 450 m est représentée par 3 cm.
On commence par convertir la distance réelle en centimètres.
450 m = 45 000 cm
On sait donc que :
3 cm sur le plan → 45 000 cm dans la réalité
Pour trouver l’échelle, on ramène la distance sur le plan à 1 cm.
3 cm sur le plan → 1 cm sur le plan
(cela signifie que l’on divise par 3)
On applique la même opération à la distance réelle.
45 000 cm → 15 000 cm
On obtient alors :
1 cm sur le plan → 15 000 cm dans la réalité
L’échelle du plan est donc 1 : 15 000.
À retenir
Pour déterminer une échelle, on ramène toujours la distance sur le plan à 1 cm, puis on lit directement l’échelle sous la forme 1 : n.
Résoudre des situations topographiques et cartographiques
Dans la proportionnalité : l’échelle d’un plan, on rencontre souvent des situations réelles liées à la lecture de cartes ou de plans. Ces situations permettent de comprendre comment une distance mesurée sur une carte correspond à une distance beaucoup plus grande dans la réalité.
Pour réussir ce type d’exercice, il est important de suivre une méthode précise. On commence par lire l’énoncé et repérer l’échelle. Ensuite, on identifie ce que l’on cherche et on vérifie les unités. Toutes les distances doivent être exprimées dans la même unité, le plus souvent en centimètres. Enfin, on applique la proportionnalité en partant de 1 cm sur le plan.
Exemple
La distance réelle entre Paris et Orléans est d’environ 130 km.
Sur une carte à l’échelle 1 : 1 000 000, on cherche la distance entre ces deux villes sur la carte.
On commence par convertir la distance réelle en centimètres.
130 km = 13 000 000 cm
On sait que :
1 cm sur le plan → 1 000 000 cm dans la réalité
On compare ensuite la distance réelle de référence à la distance réelle donnée.
1 000 000 cm → 13 000 000 cm
(cela signifie que l’on passe de la distance réelle correspondant à 1 cm sur le plan à la distance réelle donnée)
Pour passer de 1 000 000 à 13 000 000, on multiplie par 13.
On applique la même opération sur le plan.
1 cm sur le plan → 13 cm sur le plan
La distance entre Paris et Orléans sur la carte est donc 13 cm.
À retenir
Dans les situations topographiques et cartographiques, on part toujours de 1 cm sur le plan, on respecte les conversions et on applique la même proportion pour trouver la distance recherchée.
Méthode à retenir
Pour résoudre un exercice sur la proportionnalité : l’échelle d’un plan, il est important de toujours suivre la même méthode, étape par étape.
On commence par lire attentivement l’énoncé et repérer l’échelle donnée.
Ensuite, on précise ce que l’on cherche : une distance réelle, une distance sur le plan ou l’échelle du plan.
Toutes les distances doivent être dans la même unité, le plus souvent le centimètre. Il faut donc convertir les mètres ou les kilomètres en centimètres avant de calculer.
On écrit ensuite la correspondance de référence.
1 cm sur le plan correspond à un certain nombre de centimètres dans la réalité.
On applique la proportionnalité en utilisant des flèches pour passer de la valeur de référence à la valeur cherchée.
Enfin, on convertit le résultat dans l’unité demandée et on vérifie si la réponse est logique par rapport à la situation.
Exercices d’application (niveau C6)
Exercice 1 : distance réelle à partir d’un plan
Sur une carte à l’échelle 1 : 50 000, la distance entre deux points est de 6 cm.
- Écris la correspondance de référence.
- Calcule la distance réelle en centimètres.
- Convertis la distance réelle en kilomètres.
Exercice 2 : distance sur un plan à partir de la distance réelle
La distance réelle entre deux villes est de 180 km.
La carte est à l’échelle 1 : 1 000 000.
- Convertis la distance réelle en centimètres.
- Écris la correspondance de référence.
- Calcule la distance sur la carte en centimètres.
Exercice 3 : déterminer l’échelle d’un plan
Sur un plan, une route mesure 4 cm.
La distance réelle correspondante est de 2 km.
- Convertis la distance réelle en centimètres.
- Écris la correspondance entre le plan et la réalité.
- Détermine l’échelle du plan.
Exercice 4 : situation de la vie quotidienne
Un plan de jardin représente une allée de 3 cm.
La longueur réelle de cette allée est de 15 m.
- Convertis la longueur réelle en centimètres.
- Détermine l’échelle du plan.
- Écris l’échelle sous la forme 1 : n.
Corrigés détaillés
Correction de l’exercice 1
Échelle : 1 : 50 000
Distance sur la carte : 6 cm
On sait que :
1 cm sur le plan → 50 000 cm dans la réalité
On passe de 1 cm à 6 cm sur le plan.
1 cm sur le plan → 6 cm sur le plan
(cela signifie que l’on multiplie par 6)
On applique la même opération dans la réalité.
50 000 cm → 6 × 50 000 cm = 300 000 cm
On convertit en kilomètres.
300 000 cm = 3 km
La distance réelle est donc 3 km.
Correction de l’exercice 2
Distance réelle : 180 km
Échelle : 1 : 1 000 000
On commence par convertir la distance réelle en centimètres.
180 km = 18 000 000 cm
On sait que :
1 cm sur le plan → 1 000 000 cm dans la réalité
On compare la distance réelle de référence à la distance réelle donnée.
1 000 000 cm → 18 000 000 cm
(cela signifie que l’on multiplie par 18)
On applique la même opération sur le plan.
1 cm sur le plan → 18 cm sur le plan
La distance sur la carte est donc 18 cm.
Correction de l’exercice 3
Distance sur le plan : 4 cm
Distance réelle : 2 km
On commence par convertir la distance réelle en centimètres.
2 km = 200 000 cm
On écrit la correspondance.
4 cm sur le plan → 200 000 cm dans la réalité
On ramène la distance sur le plan à 1 cm.
4 cm sur le plan → 1 cm sur le plan
(cela signifie que l’on divise par 4)
On applique la même opération à la distance réelle.
200 000 cm → 50 000 cm
On obtient donc :
1 cm sur le plan → 50 000 cm dans la réalité
L’échelle du plan est 1 : 50 000.
Correction de l’exercice 4
Longueur sur le plan : 3 cm
Longueur réelle : 15 m
On convertit la longueur réelle en centimètres.
15 m = 1 500 cm
On écrit la correspondance.
3 cm sur le plan → 1 500 cm dans la réalité
On ramène la distance sur le plan à 1 cm.
3 cm sur le plan → 1 cm sur le plan
(cela signifie que l’on divise par 3)
On applique la même opération à la distance réelle.
1 500 cm → 500 cm
On obtient donc :
1 cm sur le plan → 500 cm dans la réalité
L’échelle du plan est 1 : 500.
Erreurs fréquentes
Lorsqu’on travaille sur la proportionnalité : l’échelle d’un plan, certaines erreurs reviennent souvent chez les élèves. Les connaître permet de mieux les éviter.
La première erreur consiste à oublier de convertir les unités. Par exemple, travailler avec des mètres ou des kilomètres alors que le plan est en centimètres conduit à un résultat faux.
Une autre erreur fréquente est de confondre la distance sur le plan et la distance réelle. Il faut toujours bien distinguer ce qui est mesuré sur la carte de ce qui correspond à la réalité.
Certains élèves se trompent aussi dans l’opération à effectuer. Ils multiplient au lieu de diviser, ou l’inverse, parce qu’ils n’ont pas clairement identifié ce qu’ils cherchent.
Enfin, il arrive que l’élève ne ramène pas la distance sur le plan à 1 cm lorsqu’il doit déterminer l’échelle, ce qui empêche d’écrire correctement l’échelle sous la forme 1 : n.
Mot du prof
L’échelle d’un plan peut sembler difficile au début, mais avec une méthode claire, elle devient simple. L’essentiel est de bien lire l’énoncé, de faire attention aux unités et de toujours commencer par la correspondance 1 cm sur le plan.
Prends ton temps pour construire le raisonnement étape par étape. Les erreurs font partie de l’apprentissage et permettent de progresser. Avec de l’entraînement et de la rigueur, tu maîtriseras facilement la proportionnalité et l’échelle d’un plan.
Conseils pour les parents et les professeurs
Pour aider l’élève à comprendre la proportionnalité : l’échelle d’un plan, il est important de privilégier les situations concrètes. Utiliser des cartes, des plans ou des dessins réels permet de donner du sens aux calculs.
À la maison, les parents peuvent proposer de mesurer des distances simples sur un plan ou une carte, puis de comparer ces mesures avec la réalité. L’essentiel est d’insister sur la conversion des unités et sur l’utilisation d’une méthode claire et régulière.
En classe, les professeurs peuvent encourager l’usage du tableau de proportionnalité et demander aux élèves d’expliquer leur raisonnement à l’oral. La répétition de la démarche et la variété des situations renforcent la compréhension et la maîtrise de l’échelle.
Télécharger la fiche PDF
Pour réviser efficacement la proportionnalité : l’échelle d’un plan, une fiche PDF est mise à disposition. Elle regroupe l’essentiel de la leçon, la méthode à retenir, des exercices variés et leurs corrigés détaillés.
Cette fiche permet à l’élève de s’entraîner à son rythme, de revoir les conversions d’unités et de consolider la démarche de proportionnalité. Elle peut être utilisée aussi bien en classe qu’à la maison.
Le document est prêt à être imprimé et constitue un support pratique pour la révision et l’entraînement.
Résumé de la leçon
L’échelle d’un plan permet de représenter des distances réelles sur un plan ou sur une carte en respectant la proportionnalité. Elle s’écrit le plus souvent sous la forme 1 : n, ce qui signifie que 1 cm sur le plan correspond à n cm dans la réalité.
Pour résoudre un exercice sur l’échelle d’un plan, il faut toujours commencer par mettre les distances dans la même unité, généralement le centimètre. On utilise ensuite un raisonnement de proportionnalité en partant de 1 cm sur le plan, puis on applique la même opération pour trouver la distance recherchée ou l’échelle du plan.
L’utilisation d’une méthode claire, des conversions correctes et du tableau de proportionnalité permet d’éviter les erreurs et de réussir les exercices liés à l’échelle d’un plan.
Conclusion
La proportionnalité : l’échelle d’un plan est une notion essentielle pour comprendre les plans et les cartes du quotidien. Elle permet de relier une représentation réduite à la réalité en respectant des règles simples de proportionnalité et de conversion des unités.
Grâce à une méthode claire et des exercices progressifs, l’élève peut appliquer l’échelle d’un plan dans des situations concrètes, à l’école comme dans la vie courante. Cette leçon constitue également une ressource utile à partager ou à retrouver plus tard, notamment sur Pinterest, pour réviser facilement et renforcer les acquis.
FAQ, Proportionnalité : l’échelle d’un plan.
Qu’est-ce que l’échelle d’un plan
L’échelle d’un plan est le rapport entre une distance mesurée sur un plan et la distance réelle correspondante. Elle permet de représenter la réalité de façon proportionnelle.
Comment lire une échelle écrite sous la forme 1 : n
Une échelle 1 : n signifie que 1 cm sur le plan correspond à n centimètres dans la réalité.
Pourquoi faut-il convertir les unités avant de calculer
Les calculs de proportionnalité ne sont corrects que si toutes les distances sont exprimées dans la même unité, généralement le centimètre.
Quand faut-il multiplier et quand faut-il diviser
On multiplie lorsque l’on cherche la distance réelle à partir du plan. On divise lorsque l’on cherche la distance sur le plan à partir de la distance réelle.
Comment déterminer l’échelle d’un plan
On ramène la distance sur le plan à 1 cm, puis on lit directement la distance réelle correspondante pour écrire l’échelle sous la forme 1 : n.
À quoi sert l’échelle d’un plan dans la vie quotidienne
Elle sert à lire des cartes, comprendre des plans de maisons, mesurer des distances entre des lieux et interpréter des représentations réduites de la réalité.