La proportionnalité : pourcentage est une notion essentielle en mathématiques, que l’on rencontre très souvent dans la vie quotidienne. Calculer un pourcentage permet par exemple de connaître une augmentation de salaire, une réduction de prix, la part d’une population ou encore une surface occupée, comme celle des mers et des océans sur la Terre.
Dans cette leçon, tu vas apprendre à comprendre le pourcentage comme une situation de proportionnalité, à l’écrire sous forme de fraction ou de nombre décimal, et surtout à l’utiliser pour résoudre des problèmes concrets. Grâce à des méthodes simples, notamment le tableau de proportionnalité, tu verras comment calculer facilement un pourcentage, une augmentation ou une diminution.
Ce cours propose des explications claires, des exemples guidés, des exercices progressifs avec correction, ainsi qu’une fiche PDF à télécharger pour s’entraîner et réviser efficacement.
Table of Contents
Objectifs de la leçon
À la fin de cette leçon sur la proportionnalité : pourcentage, l’élève sera capable de :
- comprendre ce qu’est un pourcentage et ce qu’il représente ;
- écrire un pourcentage sous forme de fraction ou de nombre décimal ;
- reconnaître une situation de proportionnalité liée au pourcentage ;
- utiliser correctement un tableau de proportionnalité pour calculer un pourcentage ;
- calculer un pourcentage d’une quantité ;
- résoudre des problèmes d’augmentation et de diminution en pourcentage ;
- lire et exploiter un tableau de pourcentages dans des situations concrètes.
Qu’est-ce qu’un pourcentage ?
Un pourcentage permet d’exprimer une partie d’un tout en la comparant à 100.
Le mot pourcentage signifie tout simplement « pour cent », c’est-à-dire sur 100.
Par exemple :
- 25 % signifie 25 pour 100 .
- 50 % représente la moitié .
- 100 % correspond au tout entier.
En mathématiques, le pourcentage est une situation de proportionnalité, car on compare toujours une quantité à un total de référence égal à 100. Cela permet de comparer facilement des quantités, même si les totaux sont différents.
Exemple :
Dire que 70 % de la surface de la Terre est recouverte d’eau signifie que, sur 100 parts égales, 70 parts représentent les mers et les océans.
Pourcentage, fraction et nombre décimal
Un pourcentage peut toujours être écrit sous forme de fraction ou de nombre décimal. Ces trois écritures représentent la même quantité, mais sous des formes différentes.
Du pourcentage à la fraction
Pour passer d’un pourcentage à une fraction, on écrit le nombre sur 100.
- 25 % = 25 / 100
- 60 % = 60 / 100
- 75 % = 75 / 100 = 3 / 4
Du pourcentage au nombre décimal
Pour passer d’un pourcentage à un nombre décimal, on divise par 100.
- 25 % = 0,25
- 60 % = 0,6
- 75 % = 0,75
De la fraction au pourcentage
Pour transformer une fraction en pourcentage, on la met sur 100 ou on multiplie par 100.
- 36 / 45 = 80 %
- 24 / 40 = 60 %
Comprendre ces transformations est très important pour résoudre des problèmes de proportionnalité avec des pourcentages, notamment lors des calculs d’augmentation ou de diminution.
Le tableau de proportionnalité pour calculer un pourcentage
Dans les situations de proportionnalité : pourcentage, le tableau de proportionnalité est une méthode très efficace pour comprendre et organiser les calculs.
Le principe est simple. On compare toujours une quantité à 100, car un pourcentage signifie « pour 100 ».
Méthode avec le tableau de proportionnalité
On commence par écrire les données dans un tableau.
On place 100 dans une colonne, car le pourcentage se réfère toujours à 100.
Exemple
Dans une entreprise de 450 employés, 360 sont des femmes. Quel est le pourcentage de femmes ?
On construit le tableau de proportionnalité :
450 employés correspondent à 100 %.
360 employés correspondent à x %.
On cherche la valeur de x.
Pour passer de 450 à 100, on divise par 4,5.
On applique la même opération à 360.
360 ÷ 4,5 = 80
Le pourcentage de femmes est donc de 80 %.
Cette méthode permet de visualiser clairement la proportionnalité et d’éviter les erreurs de calcul, surtout lorsque les nombres sont importants.
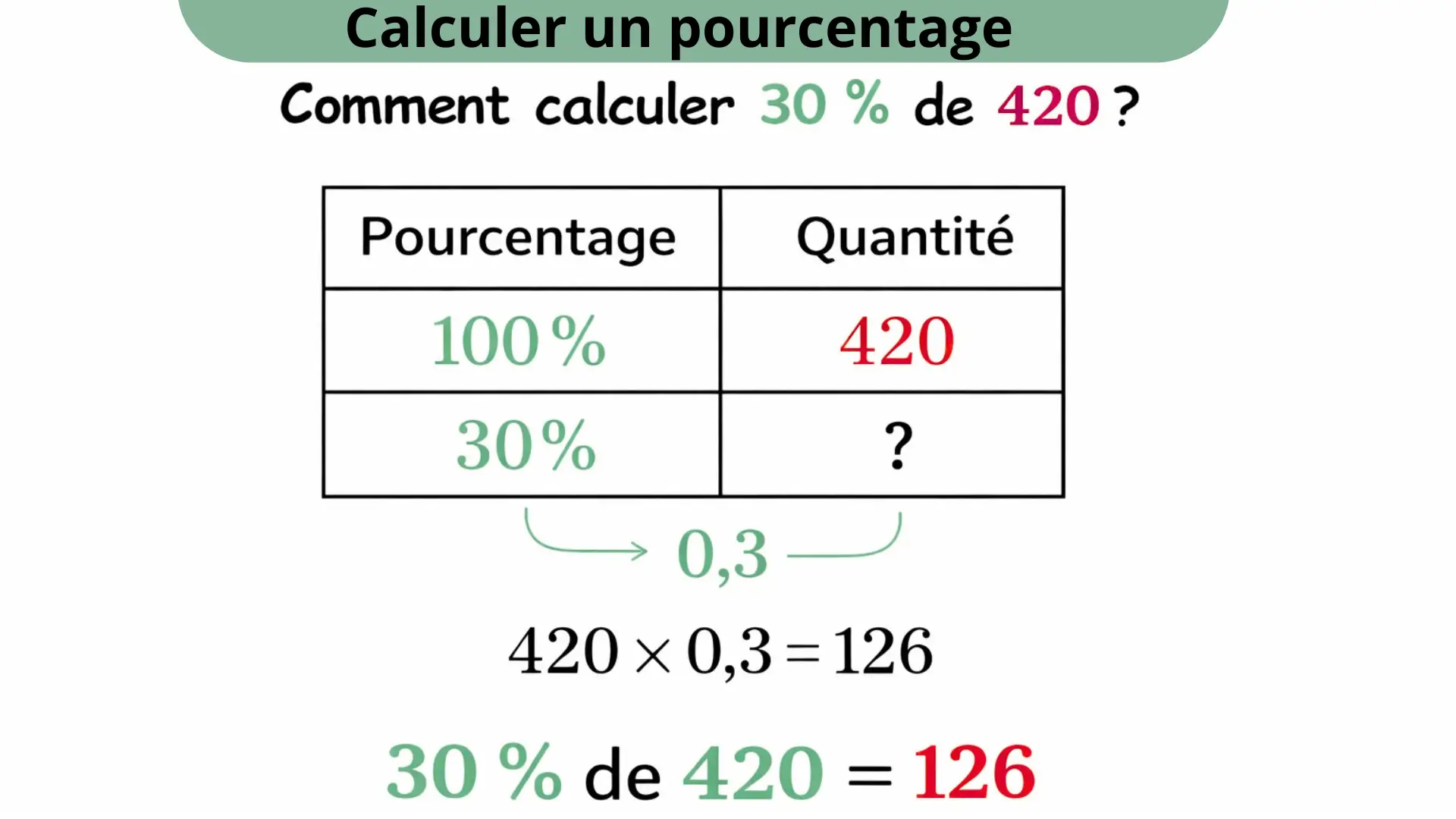
Calculer un pourcentage d’une quantité
Pour calculer un pourcentage d’une quantité, on cherche une partie d’un tout en utilisant la proportionnalité. Cette situation apparaît très souvent dans la vie quotidienne, par exemple pour calculer une réduction, une augmentation ou une part d’un ensemble.
Méthode par le calcul
Un pourcentage peut être écrit sous forme de fraction sur 100.
Ainsi, p % signifie p / 100.
Pour calculer p % d’une quantité, on multiplie la quantité par p / 100.
Exemple
La surface de la Terre est d’environ 510 millions de kilomètres carrés.
On sait que 70 % de cette surface est recouverte d’eau.
70 % = 70 / 100 = 0,7
Surface occupée par l’eau
510 × 0,7 = 357
Environ 357 millions de kilomètres carrés de la surface de la Terre sont recouverts par les mers et les océans.
Cette méthode est rapide et efficace, surtout lorsque le pourcentage est facile à transformer en nombre décimal.
Augmentation et diminution en pourcentage
Dans de nombreuses situations, un pourcentage sert à exprimer une augmentation ou une diminution d’une quantité. Ces situations sont aussi des cas de proportionnalité : pourcentage.
Augmentation en pourcentage
Une augmentation correspond à une valeur qui augmente par rapport à une valeur initiale.
Pour calculer une augmentation en pourcentage, on procède en deux étapes.
On calcule d’abord le montant de l’augmentation, puis on calcule la nouvelle valeur.
Exemple
Un salarié gagne 4 000 euros par mois. Son salaire augmente de 10 %.
10 % = 10 / 100 = 0,1
Montant de l’augmentation
4 000 × 0,1 = 400
Nouveau salaire
4 000 + 400 = 4 400 euros
Le salaire a donc augmenté de 10 %, ce qui correspond à 400 euros.
Diminution en pourcentage
Une diminution correspond à une valeur qui baisse par rapport à une valeur initiale.
On calcule d’abord le montant de la diminution, puis la nouvelle valeur.
Exemple
Le prix d’un produit était de 8 400 dirhams et passe à 6 300 dirhams.
Montant de la diminution
8 400 − 6 300 = 2 100
Pourcentage de diminution
2 100 ÷ 8 400 = 0,25
0,25 = 25 %
Le prix a donc diminué de 25 %.
Ces calculs montrent que les augmentations et les diminutions sont toujours liées à la valeur de départ, ce qui confirme qu’il s’agit bien de situations de proportionnalité.
Lire et exploiter un tableau de pourcentages
Un tableau de pourcentages permet de représenter la répartition d’un ensemble en différentes parties. Chaque valeur indique la part occupée par une catégorie par rapport au total, exprimée en pourcentage. Ce type de tableau est très utilisé en statistiques et correspond à une situation de proportionnalité : pourcentage.
Lecture d’un tableau de pourcentages
Pour lire correctement un tableau de pourcentages, il faut d’abord identifier le total, qui correspond à 100 %. Ensuite, chaque pourcentage indique la part de chaque catégorie.
Exemple
Dans un tableau qui présente la répartition des groupes sanguins d’une population, chaque pourcentage indique la proportion de personnes appartenant à un groupe donné.
Si le groupe O représente 45 %, cela signifie que, sur 100 personnes, 45 ont le groupe sanguin O.
Exploiter un tableau de pourcentages
Un tableau de pourcentages peut servir à répondre à différentes questions.
On peut comparer les catégories entre elles, déterminer la catégorie la plus représentée ou calculer un effectif à partir d’un pourcentage.
Exemple
Dans une population de 2 000 personnes, 45 % appartiennent au groupe sanguin O.
45 % = 45 / 100 = 0,45
Nombre de personnes du groupe O
2 000 × 0,45 = 900
Il y a donc 900 personnes du groupe sanguin O dans cette population.
Savoir lire et exploiter un tableau de pourcentages est indispensable pour comprendre et résoudre de nombreux problèmes de proportionnalité.
Exercices d’application
Les exercices suivants permettent de s’entraîner à utiliser la proportionnalité : pourcentage dans des situations concrètes. Ils doivent être résolus sans aide, en appliquant les méthodes vues dans le cours.
Exercice 1
La surface totale d’un pays est de 120 000 km².
Les forêts occupent 35 % de cette surface.
Calcule la surface occupée par les forêts.
Exercice 2
Dans un collège, il y a 800 élèves.
60 % des élèves sont des filles.
Calcule le nombre de filles dans ce collège.

Exercice 3
Un article coûte 250 euros.
Pendant les soldes, le prix baisse de 20 %.
Calcule le montant de la réduction puis le nouveau prix de l’article.
Exercice 4
Le prix d’un téléphone augmente de 15 %.
Son prix initial est de 1 200 euros.
Calcule le montant de l’augmentation et le nouveau prix.
Exercice 5
Dans une entreprise, 72 employés sur 90 ont suivi une formation.
Exprime cette situation en pourcentage.
Ces exercices servent à vérifier la compréhension du cours et à maîtriser les calculs de pourcentages avant de passer aux exercices corrigés.
Exercices corrigés
Voici la correction détaillée des exercices précédents. Chaque solution est expliquée étape par étape afin de bien comprendre le raisonnement et l’utilisation de la proportionnalité : pourcentage.
Correction de l’exercice 1
Surface totale : 120 000 km²
Pourcentage de forêts : 35 %
35 % = 35 / 100 = 0,35
Surface occupée par les forêts
120 000 × 0,35 = 42 000
Les forêts occupent 42 000 km².
Correction de l’exercice 2
Nombre total d’élèves : 800
Pourcentage de filles : 60 %
60 % = 60 / 100 = 0,6
Nombre de filles
800 × 0,6 = 480
Il y a 480 filles dans ce collège.
Correction de l’exercice 3

Prix initial : 250 euros
Baisse : 20 %
20 % = 20 / 100 = 0,2
Montant de la réduction
250 × 0,2 = 50
Nouveau prix
250 − 50 = 200 euros
Le nouveau prix de l’article est 200 euros.
Correction de l’exercice 4
Prix initial : 1 200 euros
Augmentation : 15 %
15 % = 15 / 100 = 0,15
Montant de l’augmentation
1 200 × 0,15 = 180
Nouveau prix
1 200 + 180 = 1 380 euros
Le nouveau prix du téléphone est 1 380 euros.
Correction de l’exercice 5
Nombre d’employés formés : 72
Nombre total d’employés : 90
On cherche le pourcentage correspondant à 72 sur 90.
72 ÷ 90 = 0,8
0,8 = 80 %
La proportion d’employés formés est de 80 %.
Erreurs fréquentes à éviter
Dans les exercices de proportionnalité : pourcentage, certaines erreurs reviennent souvent.
Beaucoup d’élèves oublient que le pourcentage est toujours lié à 100 et ne divisent pas par 100 lors du calcul.
D’autres confondent le montant de la variation avec le pourcentage de variation, surtout dans les augmentations et diminutions.
Il arrive aussi que l’on calcule une diminution en ajoutant au lieu de soustraire, ou l’inverse.
Dans les tableaux de proportionnalité, une erreur classique consiste à mal placer la valeur 100 ou à appliquer une opération différente dans les deux lignes du tableau.
Pour éviter ces erreurs, il faut toujours identifier clairement la valeur de départ et vérifier que le résultat obtenu est logique.
Mot du prof
Pour réussir les exercices sur les pourcentages, il est important de bien comprendre le sens de la situation avant de calculer. Il faut se demander si l’on cherche une partie d’un tout, une augmentation ou une diminution.
Le tableau de proportionnalité est une méthode sûre, surtout lorsque les nombres sont complexes. En contrôle, il vaut mieux une méthode claire et bien présentée qu’un calcul rapide mais risqué.
Un bon réflexe consiste à estimer le résultat avant de calculer afin de vérifier s’il est cohérent.
Conseils pour les élèves
Prends le temps de lire attentivement l’énoncé et repère la valeur totale ainsi que le pourcentage.
Transforme toujours le pourcentage en fraction ou en nombre décimal avant de calculer.
Utilise le tableau de proportionnalité lorsque tu hésites.
Vérifie ton résultat en te demandant s’il est raisonnable par rapport à la situation.
Conseils pour les parents et les enseignants
Pour aider un élève, il est conseillé d’utiliser des exemples de la vie quotidienne comme les promotions, les notes, les salaires ou les statistiques simples.
L’objectif n’est pas seulement de trouver la bonne réponse, mais de comprendre la démarche.
Encourager l’utilisation du tableau de proportionnalité permet de renforcer le raisonnement et d’éviter l’apprentissage mécanique.
Télécharger la fiche PDF
Une fiche PDF est disponible pour réviser efficacement la proportionnalité : pourcentage.
Cette fiche contient un résumé du cours, les méthodes essentielles, des exercices d’application et leurs corrections, ainsi qu’un rappel des erreurs fréquentes.
Le PDF est prêt à être imprimé ou utilisé pour s’entraîner à la maison.
Conclusion
La proportionnalité : pourcentage est une notion essentielle qui permet de mieux comprendre de nombreuses situations de la vie quotidienne, comme les promotions, les résultats scolaires, les statistiques ou les variations de prix. En maîtrisant les méthodes de calcul et en évitant les erreurs fréquentes, les élèves gagnent en confiance et en efficacité.
Pour approfondir cette leçon et s’entraîner davantage, les supports visuels et les fiches partagées sur Pinterest constituent un excellent complément au cours, en facilitant la mémorisation et la révision à la maison.
Foire aux questions
Comment calculer rapidement un pourcentage
Il suffit de transformer le pourcentage en nombre décimal et de multiplier par la quantité.
Quand utiliser un tableau de proportionnalité
Le tableau est conseillé lorsque les données sont complexes ou lorsque l’on veut visualiser la situation.
Quelle est la différence entre augmentation et diminution
Une augmentation ajoute une valeur à la quantité initiale, tandis qu’une diminution la réduit.
Pourquoi diviser par 100
Parce qu’un pourcentage signifie toujours une comparaison à 100.