Puissance est une notion mathématique très utile qui permet d’écrire plus simplement des multiplications répétées. Dans cette leçon, tu vas découvrir ce que signifie une puissance à travers deux cas très importants : le carré d’un nombre et le cube d’un nombre.
Grâce à des exemples simples et des situations concrètes, tu apprendras à reconnaître une puissance, à l’écrire correctement et à la calculer sans difficulté. La notion de puissance permet aussi de mieux comprendre des idées comme l’aire d’un carré ou le volume d’un cube, que l’on rencontre souvent en géométrie.
Ce cours facile est accompagné d’exercices corrigés pour t’entraîner pas à pas, ainsi que d’un PDF à télécharger pour réviser tranquillement à la maison ou en classe.
Table of Contents
Qu’est-ce qu’une puissance ?
Une puissance est une façon plus courte d’écrire une multiplication répétée d’un même nombre.
Par exemple, au lieu d’écrire :
2 × 2 × 2
on peut écrire :
2³
On dit alors que 2 est élevé à la puissance 3.
Les éléments d’une puissance
Une puissance est composée de deux parties :
- la base : le nombre que l’on multiplie
- l’exposant : le nombre de fois que la base est multipliée par elle-même
Dans l’écriture 5² :
- 5 est la base
- 2 est l’exposant
Cela signifie :
5² = 5 × 5
Comment lire une puissance ?
- 2² se lit « deux au carré »
- 3³ se lit « trois au cube »
Dans cette leçon, nous allons surtout travailler avec :
- la puissance 2 (le carré)
- la puissance 3 (le cube)
Pourquoi utilise-t-on les puissances ?
Les puissances permettent :
- d’écrire plus simplement des calculs
- de gagner du temps
- de mieux comprendre certaines situations en géométrie (aire et volume)
Le carré d’un nombre
Définition
Le carré d’un nombre est le produit de ce nombre par lui-même.
On dit aussi que ce nombre est élevé à la puissance 2.
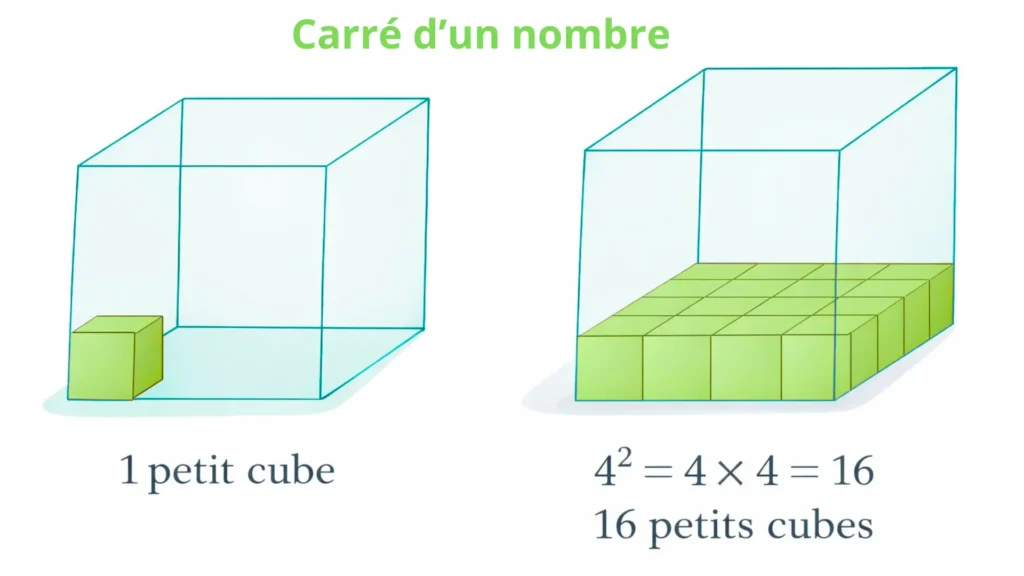
Écriture sous forme de carré
Multiplier un nombre par lui-même peut s’écrire sous forme de puissance.
Exemples :
- 4 × 4 = 4²
- 7 × 7 = 7²
- 10 × 10 = 10²
Dans chaque cas, le nombre est multiplié deux fois, c’est pour cela que l’exposant est 2.
Comment lire le carré d’un nombre ?
- 3² se lit « trois au carré »
- 6² se lit « six au carré »
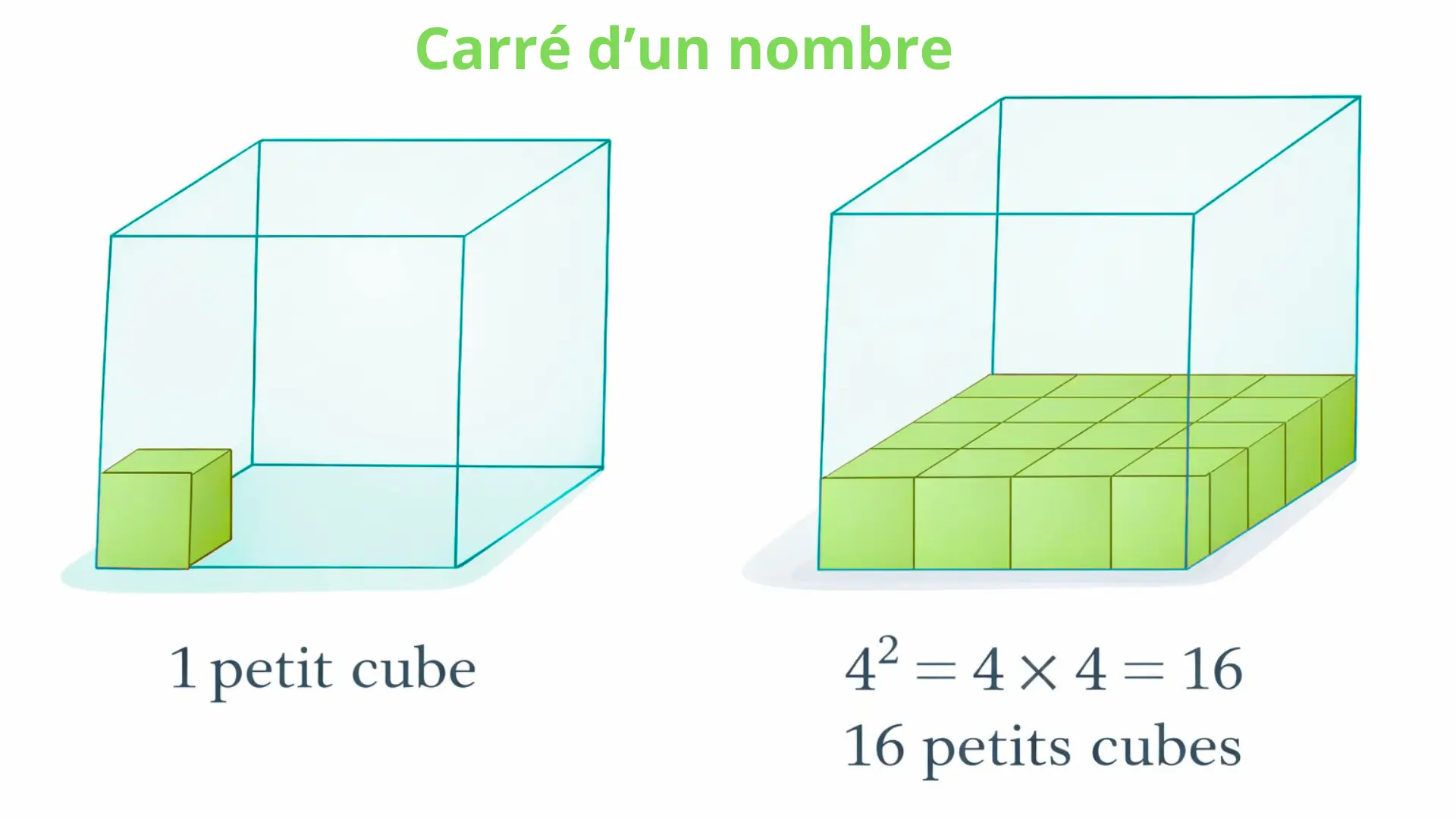
Exemple concret : aire d’un carré
Le carré d’un nombre est souvent utilisé pour calculer une aire.
Si un carré a un côté de 5 cm, alors :
- son aire est : 5 × 5 = 25
- on peut écrire : 5² = 25
Le carré d’un nombre représente donc une surface.
Le cube d’un nombre
Définition
Le cube d’un nombre est le produit de ce nombre par lui-même trois fois.
On dit aussi que ce nombre est élevé à la puissance 3.
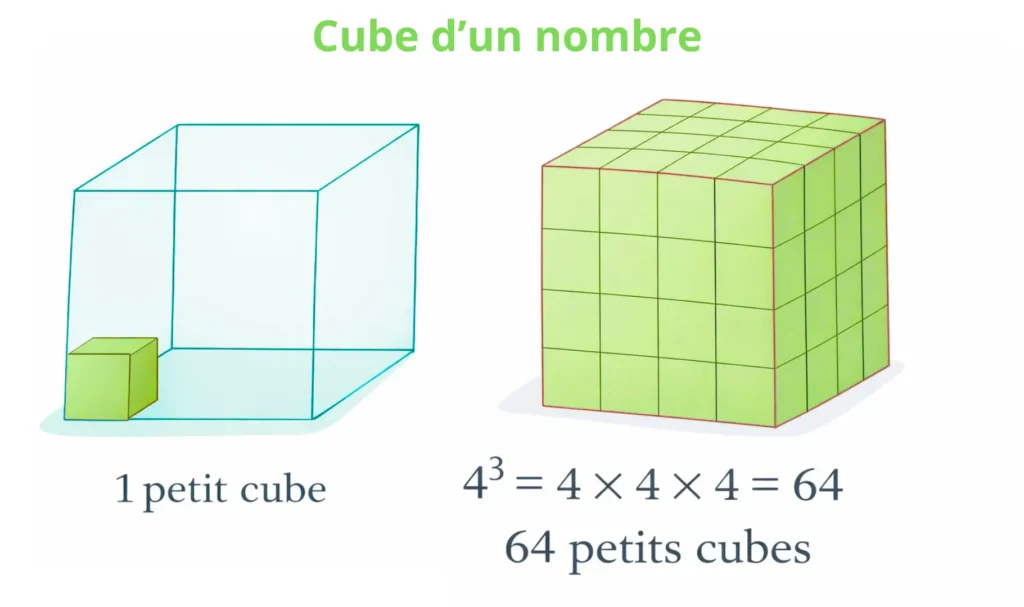
Écriture sous forme de cube
Lorsque l’on multiplie un même nombre trois fois, on peut utiliser une puissance.
Exemples :
3 × 3 × 3 = 3³
5 × 5 × 5 = 5³
2 × 2 × 2 = 2³
Dans chaque exemple, le nombre est multiplié trois fois. L’exposant est donc égal à 3.
Comment lire le cube d’un nombre
3³ se lit « trois au cube »
4³ se lit « quatre au cube »
Exemple concret volume d’un cube
Le cube d’un nombre est souvent utilisé pour calculer un volume.
Si un cube a une arête de 4 cm, alors son volume est
4 × 4 × 4 = 64
On peut écrire
4³ = 64
Le cube d’un nombre représente donc un volume.
Comparer le carré et le cube
Le carré et le cube sont deux puissances très utilisées en mathématiques. Ils ont des points communs, mais aussi des différences importantes.
Le carré d’un nombre
Le carré d’un nombre correspond à une puissance de 2.
Le nombre est multiplié par lui-même deux fois.
Exemple
5² = 5 × 5 = 25
Le carré est souvent utilisé pour calculer une surface, comme l’aire d’un carré.
Le cube d’un nombre
Le cube d’un nombre correspond à une puissance de 3.
Le nombre est multiplié par lui-même trois fois.
Exemple
3³ = 3 × 3 × 3 = 27
Le cube est souvent utilisé pour calculer un volume, comme le volume d’un cube.
Tableau comparatif
| Puissance | Écriture | Multiplication | Utilisation |
|---|---|---|---|
| Carré | n² | n × n | Aire d’un carré |
| Cube | n³ | n × n × n | Volume d’un cube |
Remarque : n est un nombre entier naturel (n = 1, 2, 3, 4, …).
À retenir
Le carré utilise la puissance 2 et sert surtout à calculer des surfaces.
Le cube utilise la puissance 3 et sert surtout à calculer des volumes.
Exercices d’application sur la puissance
Exercice 1 :
Écris chaque produit sous forme de puissance.
- 6 × 6 = ………
- 9 × 9 = ………
- 4 × 4 × 4 = ………
- 10 × 10 × 10 = ………
Exercice 2 :
Calcule les puissances suivantes.
- 5² = ………
- 8² = ………
- 3³ = ………
- 6³ = ………
Exercice 3 :
Relie chaque écriture à son calcul.
- 7²
- 2³
- 4²
a. 4 × 4
b. 2 × 2 × 2
c. 7 × 7
Exercice 4 :
Complète avec le bon nombre.
- 9² = 9 × ………
- 5³ = 5 × 5 × ………
- ………² = 16
- ………³ = 27
Exercice 5 :
Complète le tableau suivant.
| Nombre entier n | Carré de n | Cube de n |
|---|---|---|
| 2 | ……… | ……… |
| 3 | ……… | ……… |
| 5 | ……… | ……… |
| 10 | ……… | ……… |
Exercice 6 : Situation concrète
Un carré a un côté de 7 cm.
- Écris le calcul de son aire sous forme de puissance.
- Calcule cette aire.
Un cube a une arête de 3 cm.
3. Écris le calcul de son volume sous forme de puissance.
4. Calcule ce volume.
Exercice 7 Vrai ou faux
Indique si les affirmations sont vraies ou fausses.
- 6² = 6 × 2
- 4³ = 4 × 4 × 4
- Le carré d’un nombre sert à calculer une surface
- Le cube d’un nombre sert à calculer un volume
Corrigés détaillés des exercices
Correction de l’exercice 1
- 6 × 6
On multiplie 6 par lui-même deux fois.
6 × 6 = 6² - 9 × 9
Le nombre 9 est multiplié deux fois.
9 × 9 = 9² - 4 × 4 × 4
Le nombre 4 est multiplié trois fois.
4 × 4 × 4 = 4³ - 10 × 10 × 10
Le nombre 10 est multiplié trois fois.
10 × 10 × 10 = 10³
Correction de l’exercice 2
- 5²
5² = 5 × 5 = 25 - 8²
8² = 8 × 8 = 64 - 3³
3³ = 3 × 3 × 3 = 27 - 6³
6³ = 6 × 6 × 6 = 216
Correction de l’exercice 3
- 7² correspond à 7 × 7
- 2³ correspond à 2 × 2 × 2
- 4² correspond à 4 × 4
Correction de l’exercice 4
- 9² = 9 × 9
- 5³ = 5 × 5 × 5
- 4² = 16
- 3³ = 27
Correction de l’exercice 5: Tableau carré et cube
| Nombre entier n | Carré de n | Cube de n |
|---|---|---|
| 2 | 2² = 4 | 2³ = 8 |
| 3 | 3² = 9 | 3³ = 27 |
| 5 | 5² = 25 | 5³ = 125 |
| 10 | 10² = 100 | 10³ = 1000 |
Correction de l’exercice 6: Situation concrète
Carré de côté 7 cm
L’aire du carré est
7 × 7 = 7² = 49
L’aire du carré est donc 49 cm².
Cube d’arête 3 cm
Le volume du cube est
3 × 3 × 3 = 3³ = 27
Le volume du cube est donc 27 cm³.
Correction de l’exercice 7: Vrai ou faux
- 6² = 6 × 2
Faux, car 6² = 6 × 6 - 4³ = 4 × 4 × 4
Vrai - Le carré d’un nombre sert à calculer une surface
Vrai - Le cube d’un nombre sert à calculer un volume
Vrai
Erreurs fréquentes à éviter
Confondre le carré et le cube
Le carré correspond à la puissance 2 et le cube correspond à la puissance 3.
Il ne faut pas les confondre.
Exemple
4² = 4 × 4
4³ = 4 × 4 × 4
Multiplier par l’exposant
Une erreur fréquente consiste à multiplier le nombre par l’exposant.
Exemple faux
5² = 5 × 2
Exemple correct
5² = 5 × 5
Oublier le nombre de multiplications
Il faut toujours vérifier combien de fois le nombre est multiplié.
Exemple
3³ doit contenir trois fois le nombre 3
3³ = 3 × 3 × 3
Se tromper dans le calcul final
Même si l’écriture de la puissance est correcte, une erreur peut apparaître au moment du calcul.
Exemple
6² = 36 et non 12
Confondre aire et volume
Le carré est utilisé pour calculer une surface.
Le cube est utilisé pour calculer un volume.
Il faut donc faire attention aux unités
cm² pour une aire
cm³ pour un volume
À retenir
.Pour éviter les erreurs, il faut :
.calculer étape par étape.
.bien identifier la puissance utilisée,
.écrire correctement la multiplication,
Conseils pour les parents et les enseignants
Conseils pour les parents
Pour aider un enfant à comprendre cette leçon de mathématiques, il est important de partir d’exemples concrets.
Vous pouvez utiliser des objets du quotidien comme des cubes, des carreaux ou des dessins pour illustrer le carré et le cube d’un nombre.
Il est aussi conseillé de faire répéter les calculs simples, comme les carrés et les cubes des petits nombres, afin de renforcer la mémorisation.
Encouragez l’enfant à écrire la multiplication avant de calculer le résultat.
Enfin, un entraînement régulier avec des exercices courts permet de gagner en confiance et de progresser pas à pas.
Conseils pour les enseignants
Il est préférable d’introduire cette notion à partir de situations concrètes, comme l’aire d’un carré ou le volume d’un cube.
Les représentations visuelles facilitent beaucoup la compréhension, surtout au niveau C6.
Il est recommandé de commencer par les exposants 2 et 3, sans introduire trop tôt des règles complexes.
La répétition des écritures sous forme de produit puis sous forme abrégée aide les élèves à faire le lien entre les deux.
Enfin, varier les types d’exercices permet de consolider les acquis et de repérer plus facilement les difficultés des élèves.
Mot du professeur
Cette notion peut sembler nouvelle au début, mais avec un peu de pratique, elle devient rapidement accessible.
L’essentiel est de comprendre qu’elle permet d’écrire plus simplement une multiplication répétée et de calculer plus efficacement.
Téléchargement du PDF
Pour accompagner l’apprentissage de cette leçon, nous avons préparé un PDF complet à télécharger.
Ce PDF contient :
- le cours expliqué simplement,
- des exercices variés pour s’entraîner,
- les corrigés détaillés pour vérifier les réponses.
Le document est idéal pour réviser à la maison, s’entraîner en classe ou accompagner les élèves dans leur apprentissage.
Conclusion
La puissance est une notion essentielle en mathématiques qui permet d’écrire simplement des multiplications répétées. Grâce au carré et au cube d’un nombre, tu as appris à calculer des surfaces et des volumes de manière plus rapide et plus efficace.
En t’entraînant régulièrement avec les exercices et en utilisant le PDF, tu renforceras ta compréhension et tu éviteras les erreurs courantes. Cette leçon te servira aussi pour les chapitres suivants et pour résoudre des problèmes plus complexes.
Pour continuer à réviser autrement et découvrir d’autres supports visuels, tu peux également retrouver ce cours et d’autres idées pédagogiques sur pinterest, afin de t’aider à mieux mémoriser et à progresser en mathématiques.
Foire aux questions (FAQ)
Qu’est-ce qu’une puissance en mathématiques
Une puissance est une façon d’écrire une multiplication répétée d’un même nombre.
Par exemple, 4² signifie 4 × 4 et 3³ signifie 3 × 3 × 3.
Quelle est la différence entre le carré et le cube
Le carré correspond à la puissance 2 et sert surtout à calculer des surfaces.
Le cube correspond à la puissance 3 et sert surtout à calculer des volumes.
Pourquoi dit-on « au carré » et « au cube »
On dit « au carré » parce que la puissance 2 est liée à l’aire d’un carré.
On dit « au cube » parce que la puissance 3 est liée au volume d’un cube.
Faut-il apprendre par cœur les carrés et les cubes
Il est utile de mémoriser les carrés et les cubes des petits nombres, mais il est surtout important de comprendre la méthode de calcul.
À quel niveau scolaire apprend-on les puissances
Les premières puissances, le carré et le cube, sont étudiées dès le niveau C6.
Les autres seront vues plus tard au collège.