Évaluation Diagnostique en Mathématiques (1re Année Collège)

L’évaluation diagnostique est une étape essentielle en début d’année scolaire. Elle permet à l’enseignant d’identifier les acquis des élèves, de repérer leurs difficultés et de poser les bases d’un apprentissage solide.

En tant qu’enseignante de mathématiques depuis plus de quinze ans, j’ai souvent constaté que ce premier test révélait bien plus qu’un niveau scolaire. Je me souviens de Sarah, une élève qui se croyait “nulle en maths”. Lors de sa première évaluation, ses erreurs montraient surtout un manque de confiance, pas un manque de compétences. Grâce à ce diagnostic, nous avons pu travailler sur ses points faibles et elle a vite repris confiance.

C’est pour cela que je propose ici un exemple d’évaluation diagnostique en mathématiques pour la 1re année collège. Elle se compose de quatre parties :

• Activités numériques
  
• Géométrie
  
• Mesures
  
• Organisation et traitement des données

Chaque exercice est accompagné d’un objectif pédagogique et d’un conseil pour les enseignants, afin que ce test ne soit pas perçu comme une sanction, mais comme une évaluation de départ en mathématiques qui aide chaque élève à progresser.

Table of Contents

Table of Contents

Activités Numériques (17 points)

Les activités numériques constituent la base de toute évaluation diagnostique mathématiques. Elles permettent de vérifier la maîtrise des opérations fondamentales, la gestion des décimaux et l’application des règles de priorité.

1. Calculs numériques de base

Exercice :

• (42,57 – 19,248) + 3 426 = ……… (3 pts)
  
• 56,08 × 7,3 = ……… (1,5 pt)
  
• 2 145,6 ÷ 35,2 = ……… (1,5 pt)

Objectif pédagogique : Tester la précision dans les opérations avec des décimaux.

Conseil enseignant : Vérifier si l’élève aligne correctement les décimales et applique les règles de priorité.

2. Expressions et priorités des opérations

Exercice

(2/3 + 1/4) × (5/3 – 1/7) = ………………………..

(2/13 + 5/26) ÷ (4/5) = ……………………………

Objectif pédagogique : Comprendre la hiérarchie des opérations.

Conseil enseignant : Repérer les confusions entre multiplication et addition.

3. Classement de nombres décimaux

Exercice : Ranger par ordre décroissant : 0,503 – 0,5 – 12 – 0,509 – 0,498 – 2/5

Objectif pédagogique : Comparer des décimaux proches.

Conseil enseignant : Sensibiliser à la valeur des chiffres après la virgule.

 4. Décomposition en facteurs premiers

Exercice : 81 × 125 sous forme de puissances de 2 et 3.

Objectif pédagogique : Vérifier la maîtrise de la factorisation.

Conseil enseignant : Insister sur la reconnaissance des carrés et cubes parfaits.

5. Problème de vitesse et durée

Un train quitte Lyon à 7h15, arrive à Marseille à 11h00 avec un arrêt de 30 minutes. Vitesse : 90 km/h. Quelle est la distance parcourue ?

Objectif pédagogique : Relier calcul et situation réelle.

Conseil enseignant : Vérifier la maîtrise de la formule Distance = Vitesse × Temps

Géométrie (11 points)

La géométrie permet d’évaluer les compétences instrumentales (compas, règle, rapporteur) et la compréhension des propriétés des figures

 1. Cercles et quadrilatères

• Exercice : Tracer deux cercles de rayons 2,5 cm et 3,5 cm sur des droites sécantes et déterminer la nature du quadrilatère formé.
  
• Objectif pédagogique : Vérifier précision et raisonnement.
  
• Conseil enseignant : Observer si l’élève justifie sa réponse.

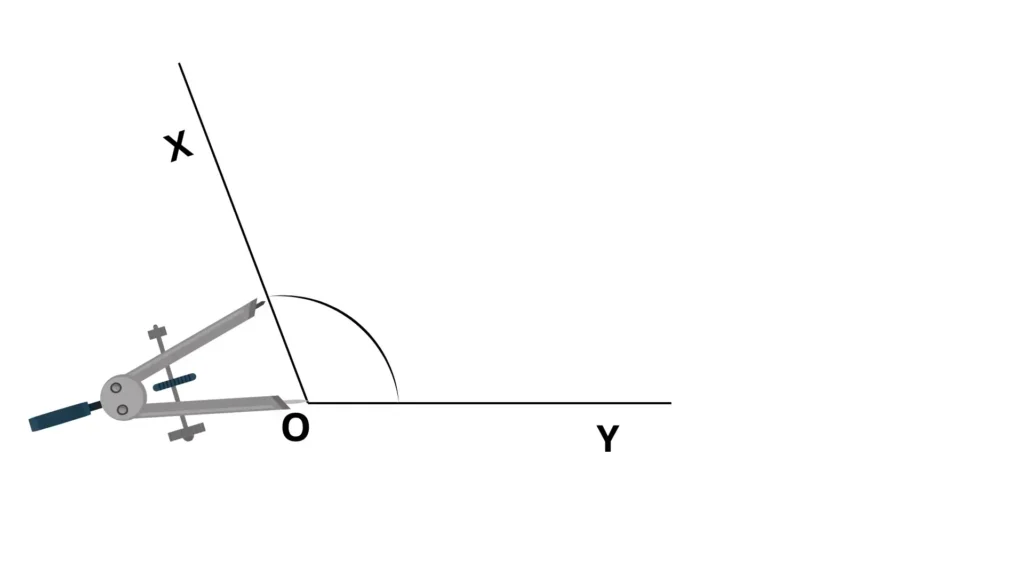
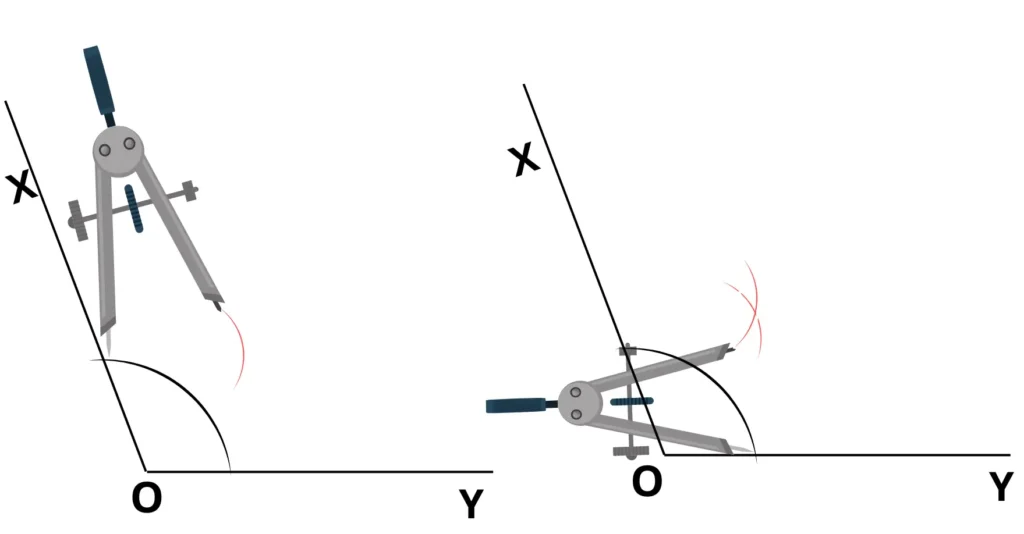
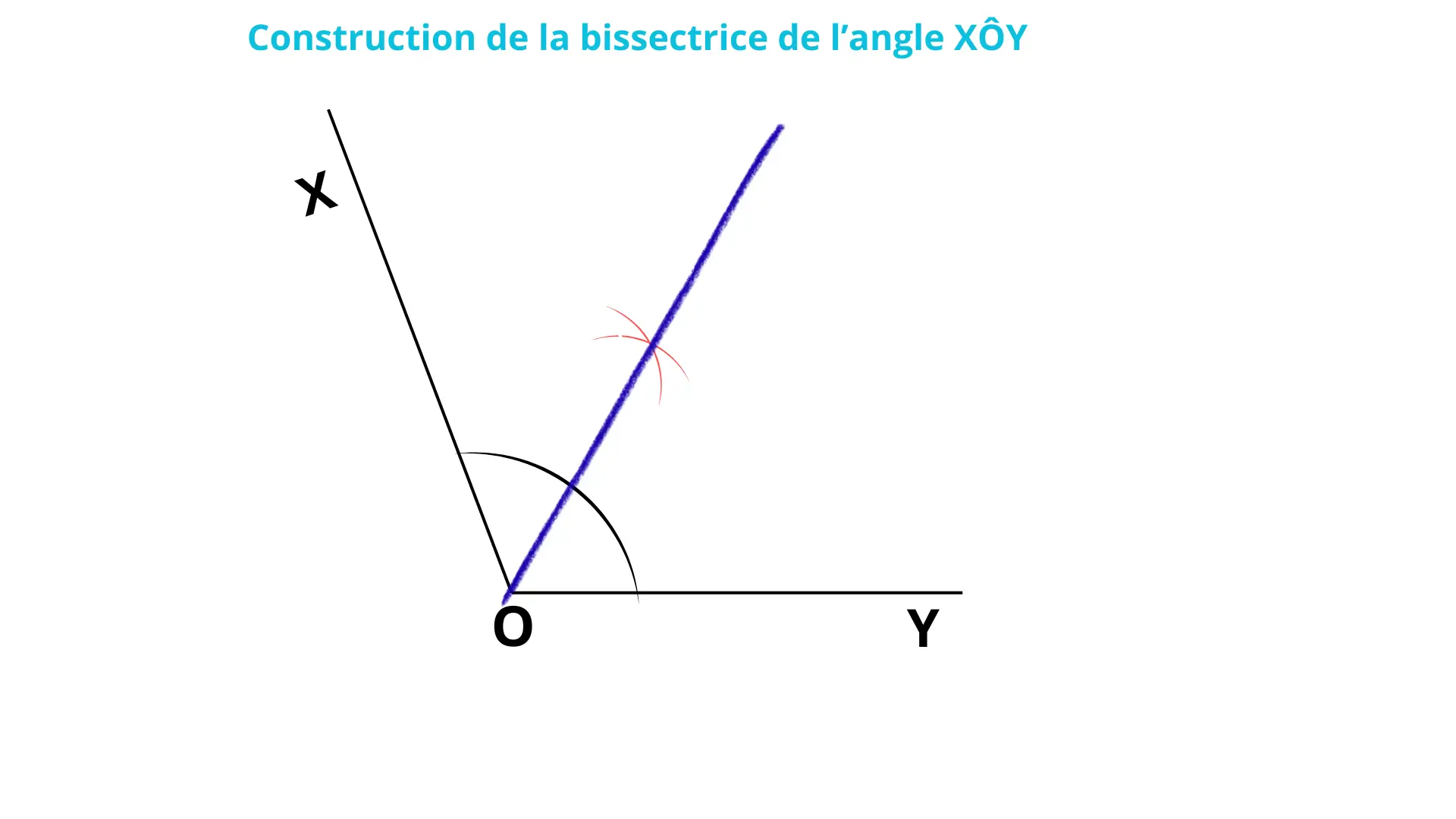
2. Angles et bissectrice

• Exercice : Tracer un angle de 120° et sa bissectrice.
  
• Objectif pédagogique : Comprendre la notion de partage d’un angle.
  
• Conseil enseignant : Vérifier l’utilisation du rapporteur.

3. Construction d’un losange

• Exercice : Construire un losange EF = 5 cm, angle = 70°.
  
• Objectif pédagogique : Combiner mesure et construction.

Conseil enseignant : Vérifier la connaissance des propriétés du losange.

 4. Symétrie axiale

• Exercice : Tracer le symétrique d’une figure par rapport à un axe.
  
• Objectif pédagogique : Vérifier la maîtrise de la symétrie.

Conseil enseignant : Observer la conservation des distances.

Activités de Mesures (8 points)

Les mesures permettent de tester les conversions et l’application des formules dans des contextes concrets.

 1. Conversions d’unités

• Exercice : Convertir des longueurs, masses, aires et volumes (m, hm, cm → dm ; t, q, hg → kg ; km², a, dm² → ca ; dl, dm³, ml → cl).
  
• Objectif pédagogique : Vérifier les relations entre unités.
  
• Conseil enseignant : Identifier les confusions fréquentes (kg ↔ g, cm ↔ m).

2. Aire d’un trapèze

• Exercice : Calculer l’aire réelle d’un terrain trapézoïdal à l’échelle 1/2000.
  
• Objectif pédagogique : Relier géométrie et proportionnalité.
  
• Conseil enseignant : Vérifier l’application de la formule de l’aire.

3. Volume d’un cylindre

• Exercice : Une citerne de rayon 3,2 m et hauteur 5 m est remplie aux 2/3. Calculer le volume en litres.
  
• Objectif pédagogique : Appliquer la formule V = π × r² × h.

Conseil enseignant : Vérifier la conversion m³ → L.

Organisation et Traitement des Données (4 points)

Cette partie teste la capacité à lire et exploiter un graphique.

1. Lecture d’un diagramme en barres

• Exercice : Compléter un tableau à partir d’un diagramme (théâtre, musique, danse, dessin).
  
• Questions :
  a) Quelle activité est la plus choisie ?
  b) Combien d’élèves au total ?
  
• Objectif pédagogique : Développer l’analyse de données.
  
• Conseil enseignant : Vérifier l’addition et la comparaison de valeurs.

Conclusion

L’évaluation diagnostique en mathématiques est bien plus qu’un simple test. Elle constitue un outil précieux pour comprendre les élèves, identifier leurs besoins et construire un enseignement adapté.

En tant qu’enseignante, je considère chaque évaluation diagnostique comme une opportunité : celle de montrer à mes élèves que les erreurs ne sont pas des échecs, mais des tremplins pour apprendre.  Pour aider d’autres enseignants et parents, n’hésitez pas à partager cette évaluation sur mon compte Pinterest. Vous y trouverez également d’autres fiches et exercices pratiques pour accompagner vos élèves pas à pas en mathématiques.

Téléchargez le fichier complet d’exercices d’évaluation diagnostique (format PDF)

Évaluation Diagnostique en Mathématiques

Évaluation diagnostique maths 1re année collège.Télécharger

FAQ : Évaluation Diagnostique en Mathématiques