Les triangles : propriétés et construction est un chapitre de géométrie qui permet aux élèves d’apprendre à reconnaître les différents types de triangles et à les tracer avec précision.
Un triangle est une figure géométrique formée de trois côtés, trois sommets et trois angles. Selon la longueur de ses côtés ou la mesure de ses angles, il existe plusieurs sortes de triangles : équilatéral, isocèle, quelconque, rectangle et rectangle isocèle.
Dans cette leçon, tu vas découvrir comment classer les triangles selon leurs propriétés et surtout les construire pas à pas à l’aide de la règle, du compas et de l’équerre.
À la fin, tu trouveras des exercices d’application et une fiche PDF à télécharger pour t’entraîner à la maison.
Table of Contents
Les différents types de triangles
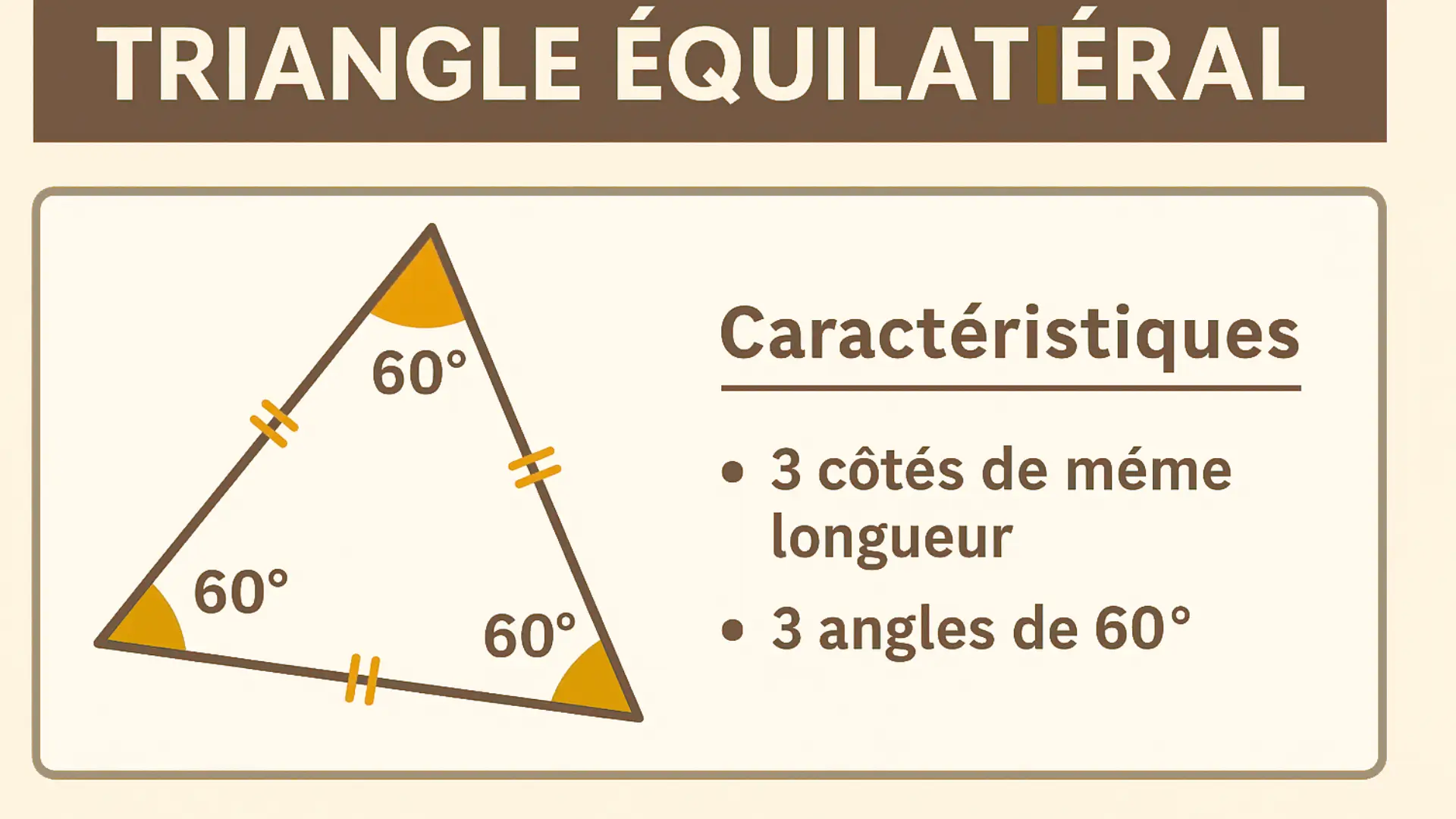
Le triangle équilatéral
Un triangle équilatéral a trois côtés de même longueur.
Ses trois angles sont aussi égaux (60° chacun).
C’est le triangle le plus régulier et le plus facile à tracer avec un compas.
Le triangle isocèle
Le triangle isocèle possède deux côtés égaux et un troisième côté différent.
Les deux angles à la base sont égaux.
C’est une forme très fréquente en géométrie et dans la vie courante (panneaux, toits, etc.).

Le triangle quelconque
Le triangle quelconque est celui dont aucun côté n’est égal à un autre.
C’est la forme la plus générale : on le rencontre souvent dans les constructions libres.
Il n’a aucune égalité entre ses côtés.
Le triangle rectangle
Un triangle rectangle possède un angle droit (90°).
On le construit à l’aide d’une équerre.
Ce type de triangle est très utilisé pour mesurer et construire.
Le triangle rectangle isocèle
Le triangle rectangle isocèle a un angle droit et deux côtés égaux.
Ses deux autres angles mesurent chacun 45°.
C’est un cas particulier du triangle rectangle.

Construction des triangles (étape par étape)
Construction d’un triangle équilatéral
- Trace un segment [AB] de 5 cm.
- Place la pointe du compas sur A, puis trace un arc de 5 cm.
- Place ensuite la pointe sur B et trace un deuxième arc qui croise le premier.
- Appelle le point d’intersection C et relie A, B et C.
Le triangle ABC est équilatéral.
Construction d’un triangle isocèle
- Trace la base [AB] = 6 cm.
- Ouvre le compas à 4 cm et trace un arc depuis A, puis un autre depuis B.
- Appelle le point d’intersection C.
- Relie A, B et C.
Le triangle ABC est isocèle.
Construction d’un triangle quelconque
- Trace un segment [AB] = 5 cm.
- Avec le compas, reporte depuis A une longueur de 4 cm, puis depuis B une longueur de 6 cm.
- Appelle C le point d’intersection.
Relie A, B et C : c’est un triangle quelconque.
Construction d’un triangle rectangle
- Trace la base [AB] = 6 cm.
- En A, construis un angle droit à l’aide de l’équerre.
- Sur ce côté, reporte une longueur de 4 cm pour placer le point C.
- Relie C à B.
Le triangle ABC est rectangle en A.

Construction d’un triangle rectangle isocèle
- En A, trace un angle droit avec l’équerre.
- Sur chaque côté de l’angle, mesure 4 cm et marque les points B et C.
- Relie B et C.
Le triangle ABC est rectangle isocèle en A.
Erreurs fréquentes
Ne pas vérifier les longueurs avec la règle.
Oublier d’utiliser le compas ou l’équerre.
Relier les mauvais points.
Ne pas respecter les mesures données.
Dessiner à main levée au lieu d’utiliser les instruments.
Confondre triangle isocèle et équilatéral.
Exercices d’application
Exercice 1 : Classe les triangles suivants selon leurs côtés.
(a) 5 cm, 5 cm, 5 cm – (b) 4 cm, 4 cm, 6 cm – (c) 3 cm, 5 cm, 7 cm
Exercice 2 : Construis les triangles suivants.
- Triangle équilatéral de 6 cm de côté
- Triangle isocèle de base 6 cm et côtés de 4 cm
- Triangle quelconque de côtés 3 cm, 4 cm, 5 cm
- Triangle rectangle en A avec AB = 6 cm et AC = 4 cm
- Triangle rectangle isocèle de 4 cm de côté
Cours clair à retenir
Un triangle a trois côtés et trois angles.
La somme des angles d’un triangle est toujours égale à 180°.
Types de triangles à connaître :
Équilatéral : trois côtés égaux
Isocèle : deux côtés égaux
Quelconque : aucun côté égal
Rectangle : un angle droit
Rectangle isocèle : un angle droit et deux côtés égaux
Fiche PDF à télécharger
Télécharge la fiche PDF complète « Les triangles : propriétés et construction » qui contient :
• le résumé du cours clair
• les exercices à imprimer
• les figures à tracer
• le corrigé en fin de page
Télécharger le PDF “Les triangles : propriétés et construction”
Mot du professeur
Chers élèves,
la géométrie demande précision, concentration et patience.
Prenez le temps d’ajuster votre compas, de bien tracer vos segments et de toujours vérifier vos mesures.
Chaque erreur devient une occasion d’apprendre.
Entraînez-vous régulièrement avec la fiche PDF : plus vous pratiquez, plus vous serez à l’aise avec les constructions.
Si certains points du cours te posent encore question ou si tu aimerais davantage d’exercices d’entraînement, partage- le dans les commentaires.
Je consulte régulièrement vos retours et enrichis le site avec de nouvelles fiches adaptées à vos besoins.
Merci pour ton engagement et ta curiosité : ce sont les clés de la réussite en mathématiques.
Conclusion
Dans cette leçon sur les triangles : propriétés et construction, tu as appris à reconnaître les principaux types de triangles et à les tracer avec méthode.
Ces notions te serviront dans de nombreux chapitres de géométrie, notamment ceux sur les quadrilatères et les polygones.
Continue à t’entraîner avec les exercices proposés et télécharge la fiche PDF pour réviser à ton rythme.
Retrouve CoursCool sur Pinterest pour découvrir chaque semaine de nouvelles fiches de révision, affiches pédagogiques et idées d’activités qui rendent les mathématiques plus claires et motivantes.
FAQ : Questions fréquentes
Comment reconnaître un triangle équilatéral
C’est un triangle dont les trois côtés ont la même longueur.
Quelle est la différence entre un triangle isocèle et un triangle quelconque
L’isocèle a deux côtés égaux, le quelconque n’a aucun côté égal.
Avec quels outils peut-on construire un triangle rectangle
Avec une règle et une équerre.
Le triangle rectangle isocèle a-t-il un angle droit
Oui, il possède un angle droit et deux côtés égaux.
Pourquoi est-il important d’apprendre à construire les triangles
Parce que la construction géométrique développe la précision, la logique et la compréhension des formes.
Pourquoi appelle-t-on un triangle qui possède un angle droit un triangle rectangle ?
On l’appelle triangle rectangle parce qu’il représente la moitié d’un rectangle.
Si l’on trace une diagonale dans un rectangle, on obtient deux triangles identiques, chacun ayant un angle droit. C’est cette particularité qui donne son nom au triangle rectangle.
Comment peut-on vérifier qu’un triangle possède un angle droit ?
Pour vérifier qu’un triangle a un angle droit, on utilise une équerre.
On place l’équerre à l’intérieur du triangle : si un des angles correspond exactement à l’angle de l’équerre, alors le triangle est rectangle.
Quelle est la différence entre un triangle isocèle et un triangle équilatéral ?
Un triangle isocèle a deux côtés égaux et un troisième différent.
Un triangle équilatéral, lui, a trois côtés égaux et trois angles égaux de 60°.
On peut dire que le triangle équilatéral est un cas particulier du triangle isocèle.
Pourquoi la somme des angles d’un triangle est-elle toujours égale à 180°
Parce qu’un triangle peut être vu comme une figure obtenue à partir d’une ligne droite.
Si on découpe les trois angles d’un triangle et qu’on les aligne côte à côte, ils forment une ligne droite, soit 180°.
C’est une propriété commune à tous les triangles, quels que soient leurs côtés ou leurs angles.
Pourquoi les deux angles à la base d’un triangle isocèle sont-ils égaux
Dans un triangle isocèle, les deux côtés égaux s’opposent à deux angles qui sont aussi égaux.
C’est une propriété géométrique : quand deux côtés ont la même longueur, les angles opposés à ces côtés ont la même mesure.